Home
Class 11
PHYSICS
A satellite is orbiting the earth of mas...

A satellite is orbiting the earth of mass `M` in equatorial plane in a circular orbit having radius `2R` and same sense of rotation as that of the Earth. Find duration of time for which a man standing on the equator will be able tosee the satellite continuously. Assume that the mans can see the satellite when it is above horizon. take Earth's angular velocity `omega`.

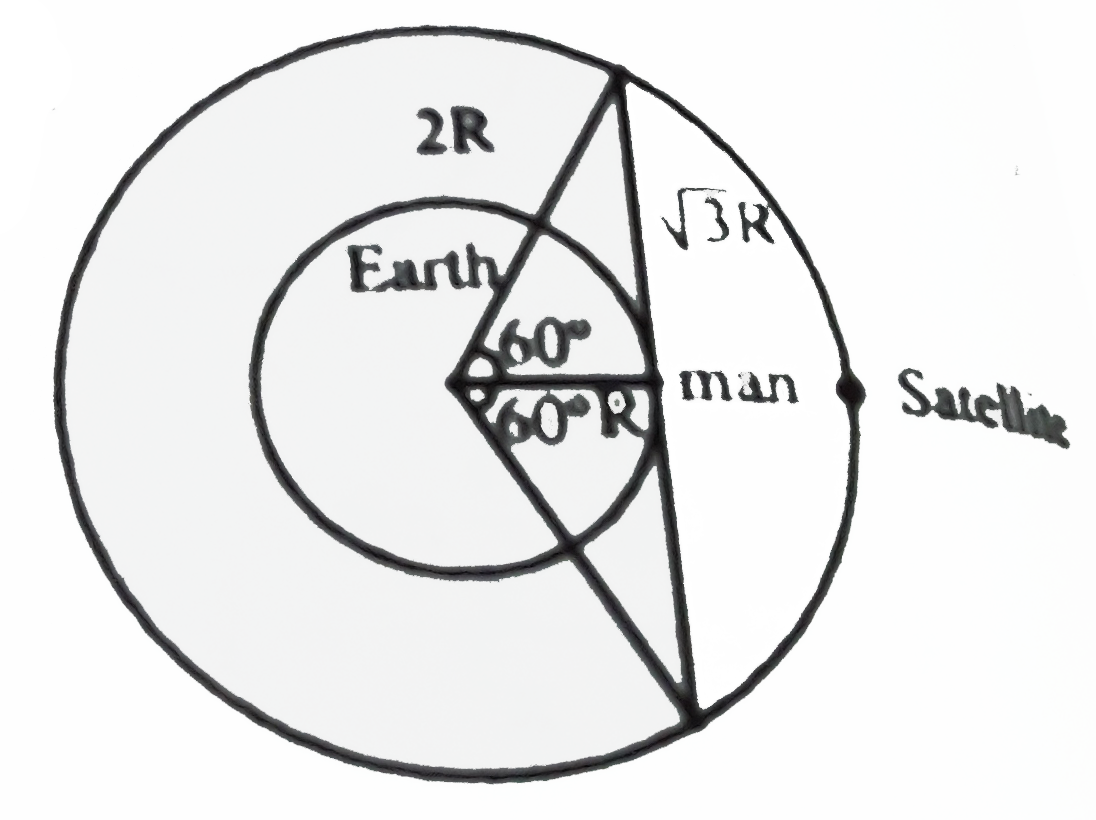
Text Solution

Verified by Experts

The correct Answer is:
`(2pi)/(3[sqrt((GM)/(8R^(3))-omega_(e))])`
`m(2R)omega^(2)=(GM_(e))/((2R)^(2))`
`omega=sqrt((GM)/(8R^(3)))`
`omega_(rel)=omega-omega_("earth")impliesomega_(rel)=sqrt((GM)/(8R^(3)))-omega_(s)`
`t=theta/(omega_(rel))impliesT=((2pi//3))/(sqrt(GM)/(8R^(3))-omega_(e))`
`t=(2pi)/(3(sqrt((GM)/(8R^(3))-omega_(e))))`
Promotional Banner

Similar Questions

Explore conceptually related problems

Two satellites of masses M and 4M are orbiting the earth in a circular orbit of radius r. Their frequencies of revolution are in the ratio of

A satellite whose mass is M , is revolving in circular orbit of radius r around the earth. Time of revolution of satellite is

A satellite of mass m moving around the earth of mass m_E in a circular orbit of radius R has angular momentum L. The rate of the area swept by the line joining the centre of the earth and satellite is

A satellite is orbiting around the earth in an orbitin equatorial plane of radius 2R_(e) where R_(e) is the radius of earth. Find the area on earth, this satellite covers for communication purpose in its complete revolution.

A satellite of mass m is revolving in a circular orbit of radius r. The relation between the angular momentum J of satellite and mass m of earth will be -

A satellite of mass M_(s) is revolving around the earth (Mass M) in a orbit of radius R. Find its angular momentum.

A satellite has to revolve round the earth in a circular orbit of radius 8 xx 10^(3) km. The velocity of projection of the satellite in this orbit will be -

A satellite of mass m is orbiting around the earth (mass M, radius R) in a circular orbital of radius 4R. It starts losing energy slowly at a constant -(dE)/(dt)=eta due to friction. Find the time (t) in which the satellite will spiral down to the surface of the earth.