Home
Class 11
PHYSICS
A body is lauched from the earth's surfa...

A body is lauched from the earth's surface a an angle `alpha=30^(@)` to the horizontal at a speed `v_(0)=sqrt((1.5 GM)/R)`. Neglecting air resistance and earth's rotation, find (a) the height to which the body will rise. (ii) the radius of curvature of trajectory at its top point.

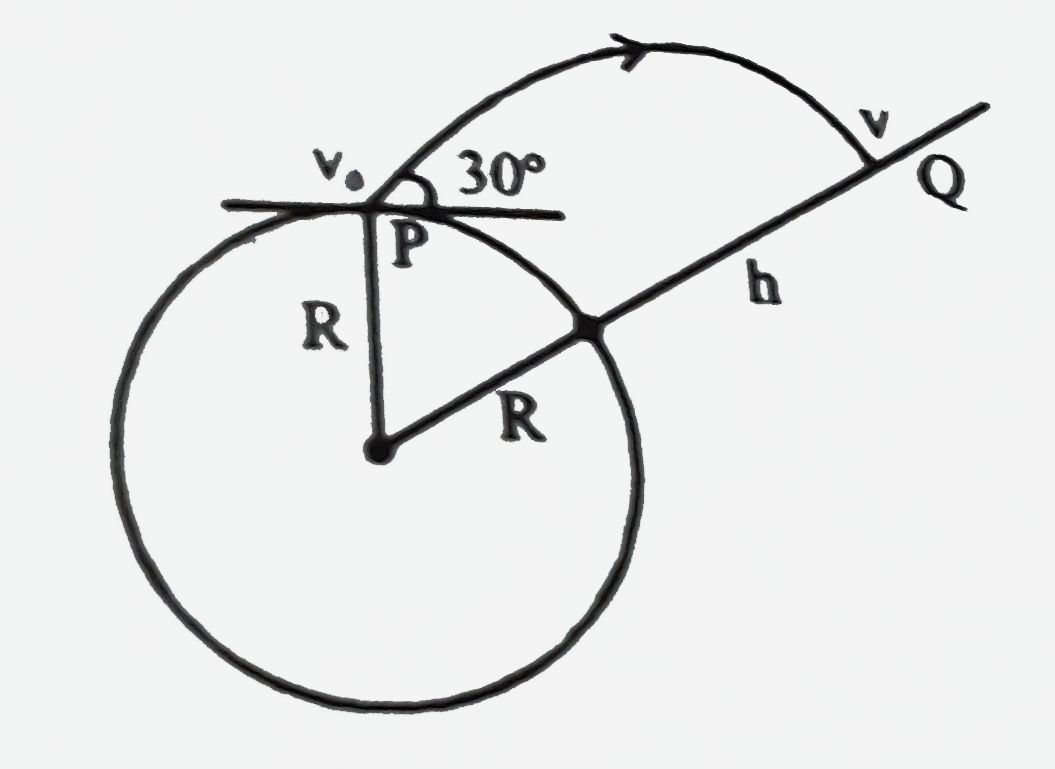
Text Solution

Verified by Experts

The correct Answer is:
`(a) h=(sqrt(7))/2+1)R,(b)1.13 R`
(a) Applying conservation of angular momentum between point `P` and `Q`

`m(v_(0)cos30^(@))R=mvr`
`v=(sqrt(3))/2(v_(0)R)/r...(1)`
Applying conservation of mechanical energy.
`-(GMm)/R+1/2mv_(0)^(2)=-(GMm)/r+1/2mv^(2)...(2)`
From `(1)` and `(2)`
`-(GMm)/R+1/2mv_(0)^(2)=-(GMm)/r+1/2m(3v_(0)^(2)R^(2))/(4r^(2))...(3)`
given that `v_(0)=sqrt(3/2(GM)/R)...(4)`
From `(3)` and `(4)`
`4r^(2)-16Rr+9R^(2)=0`
`r=2R+(sqrt(7))/2RimpliesR+h=2R+(sqrt(7))/2R`
`h=(sqrt(7)/2+1)Rimpliesh=sqrt(7)/2R`
(b) Radius of curvature `=(v^(2))/g=((sqrt(3)v_(0)R)/(2r^(2)))^(2)//(GM)/(R^(2))`
radius of curvature=`3/4(v_(0)^(2)R^(2))/(GM)`
`=3/4xx((3/2sqrt(GM)/R))^(2)xx(R^(2))/(GM)=9/8R=1.125 R`
Promotional Banner

Similar Questions

Explore conceptually related problems

A body is projected up from the surface of the earth with a velocity half the escape velocity at an angle of 30^(@) with the horizontal. Neglecting air resistance and earth’s otation, find (a) the maximum height above the earth’s surface to which the body will rise. (b) will the body move around the earth as a satellite?

A particle is fired vertically from the surface of the earth with a velocity kupsilon_(e) , where upsilon_(e) is the escape velocity and klt1 . Neglecting air resistance and assuming earth's radius as R_(e) . Calculated the height to which it will rise from the surface of the earth.

A projectile is fired from surface of earth at 30^(@) above horizontal with speed u=sqrt((GM_(c))/(R)) where M_(c) is mass of earth R is radius of earth Find maximum height of the projectile above earth surface

A body is thrown from the surface of the Earth at an angle alpha to the horizontal with the initial velocity v_0 . Assuming the air drag to be negligible, find: (a) the time of motion, (b) the maximum height of ascent and the horizontal range, at what value of the angle alpha they will be equal to each other, (c) the equation of trajectory y(x) , where y and x are displacements of the body along the vertical and the horizontal respectively, (d) the curvature radii of trajectory at its initial point and at its peak.

If R is the radius of the earth, the height at which g will decrease by 0.1% of its value at the surface of the earth is

A particle is projected at angle theta with horizontal with velocity v_0 at t = 0 . Find (a) tangential and normal acceleration of the particle at t = 0 and at highest point of its trajectory. (b) the radius of curvature att = 0 and highest point. .

STATEMENT-1: A body is projected from the ground with kinetic energy K at an angle of 60° with the horizontal. If air resistance is neglected, its K.E. When it is at the highest point of its trajectory will be K/4 because STATEMENT-2: At the highest point of the trajectory, the direction of velocity and acceleration of the body are perpendicular to each other

A body is thrown with the velocity v_0 at an angle of theta to the horizon. Determine v_0 "in" m s^-1 if the maximum height attained by the body is 5 m and at the highest point of its trajectory the radius of curvature is r = 3 m . Neglect air resistance. [Use sqrt(80) as 9] .

A body Is projected horizontally near the surface of the earth with sqrt(1.5) times the orbital velocity. Calculate the maximum height up to which it will rise above the surface of the earth.

An object is projected from the earth's surface with escape velocity at 30^(@) with horizontal. What is the angle made by the velocity with horizontal when the object reaches a height 2R from the earth's surface ? R is the radius of the earth. Horizontal can be considered as a line parallel to the tangent at the earth's surface just below the object .