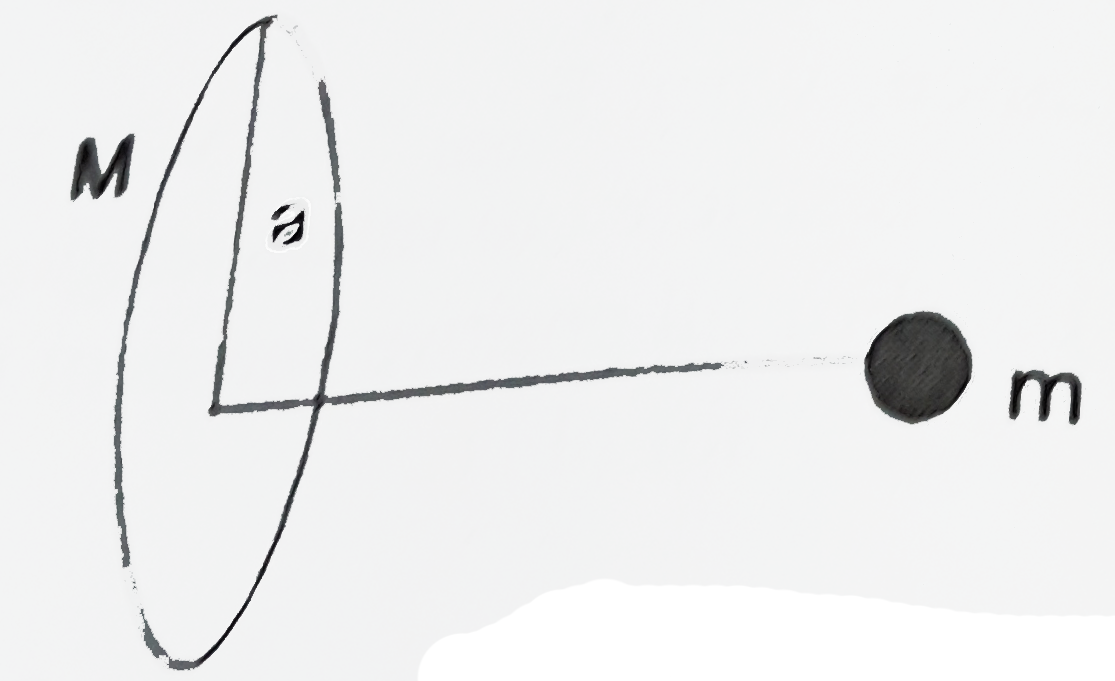
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A particle of mass m is placed at a distance x from the centre of ring...
Text Solution
|
- An impulse J is applied on a ring of mass m along a line passing throu...
Text Solution
|
- A particle of mass m is placed at a distance x from the centre of ring...
Text Solution
|
- A particle of mass m is placed at a distance x from the centre of ring...
Text Solution
|
- A particle of mass m is placed at a distance x from the centre of ring...
Text Solution
|
- A particle of mass m is placed at a distance R from centre of a unifor...
Text Solution
|
- A circular ring of mass M and radius R is placed in YZ plane with cent...
Text Solution
|
- A point particle of mass m is released from a distance sqrt(3)R along ...
Text Solution
|
- A thin wire of mass m and length l is bent in the form of a ring . Mom...
Text Solution
|