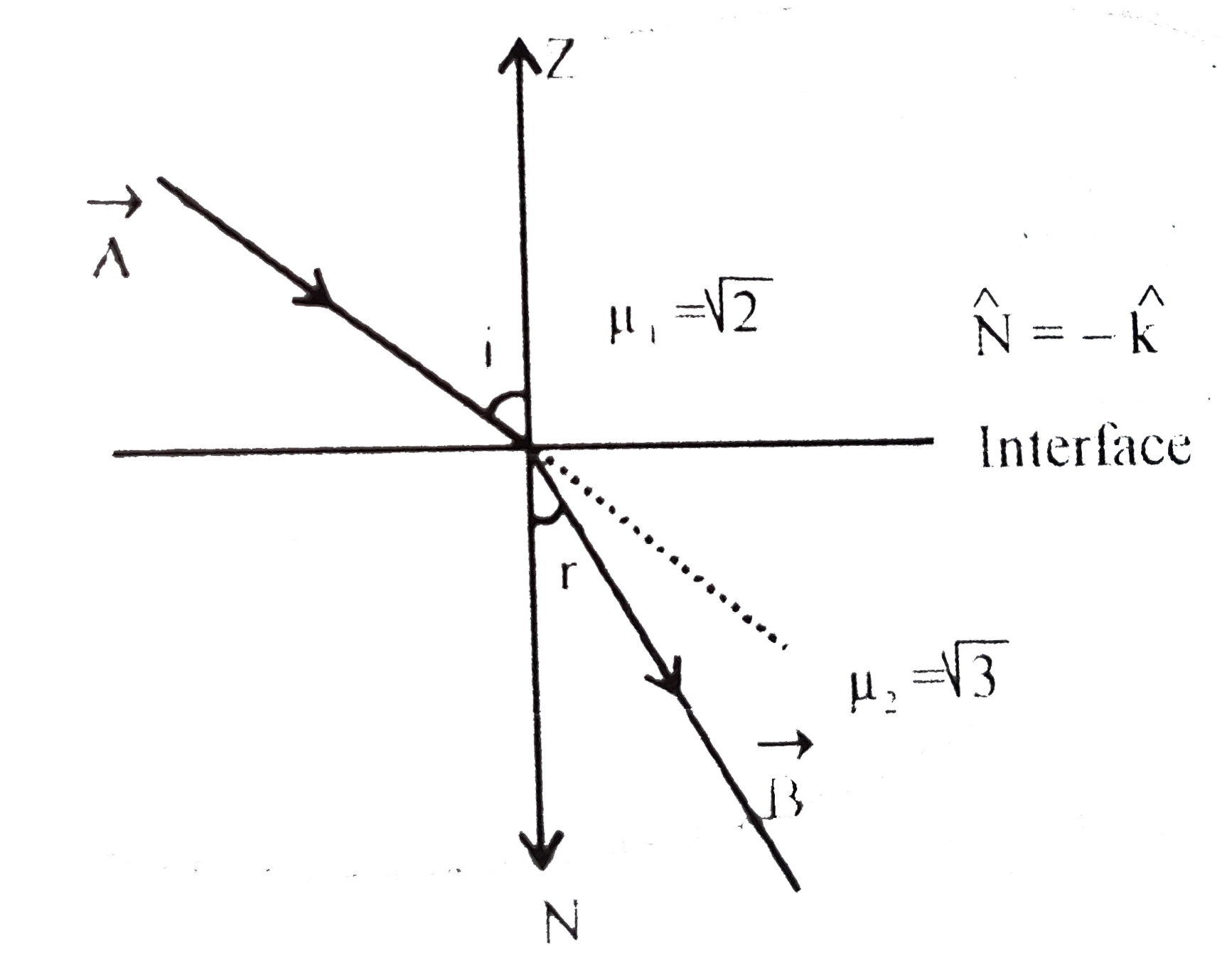
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Let the x-z plane be the boundary between two transparent media. Mediu...
Text Solution
|
- Let the x-z plane be the boundary between two transparent media. Mediu...
Text Solution
|
- Let the x-z plane be the boundary between two transparent media. Mediu...
Text Solution
|
- x-y plane separates two media, zge0 contains a medium of refractive i...
Text Solution
|
- Let the x-z plane be the boundary between two transparent media. Media...
Text Solution
|
- The x-y plane is the boundary between two transparent media. Medium-1 ...
Text Solution
|
- The x-y plane is the boundary between two transparent media. Medium-1 ...
Text Solution
|
- मान ले की दो पारदर्शी माध्यमों के बीच सीमा X -Y ताल से दी जाती है। z g...
Text Solution
|
- Let the XZ plane be the boundary between two transparent media. Medium...
Text Solution
|