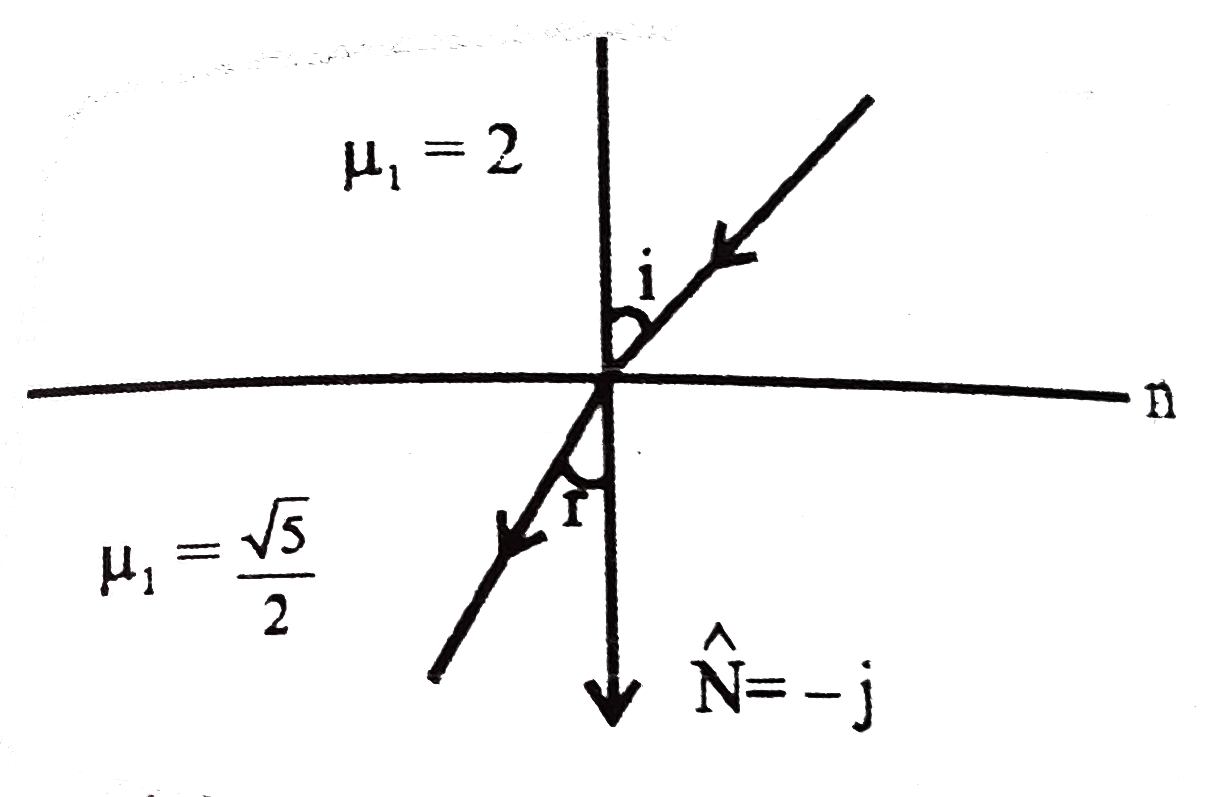
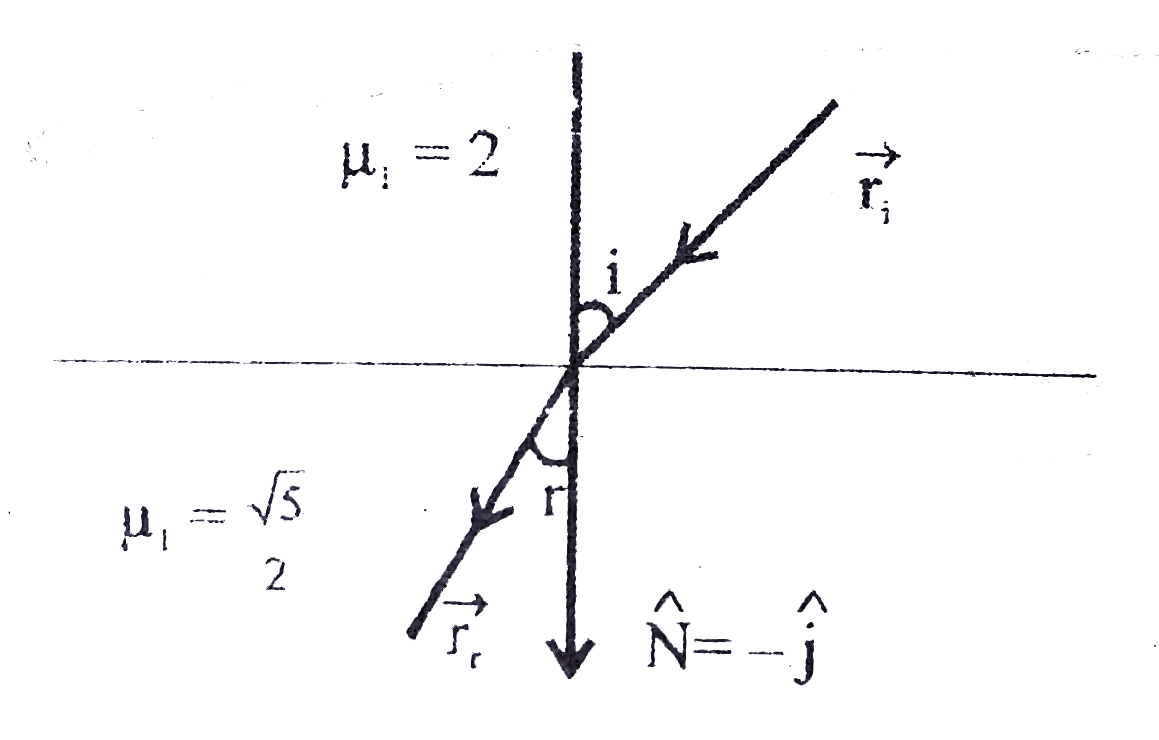A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ray of light moving along the unit vector (-i-2j)undergoes refractio...
Text Solution
|
- A unit vector along the incident ray of light is hat(i). The unit vect...
Text Solution
|
- x-y plane separates two media, zge0 contains a medium of refractive i...
Text Solution
|
- If hat(i) denotes a unit vector along incident light ray, hat (r) a un...
Text Solution
|
- A ray of light moving along the unit vector ( -i-2j )undergoes refract...
Text Solution
|
- A ray of light moving along a vector (3sqrt(2) hat(i)-3 hat(j)-3 hat(k...
Text Solution
|
- If hat(i) denotes a unit vector along incident light ray, hat( r) a un...
Text Solution
|
- If hati denotes a unit vector along incident light ray, hati a unit ve...
Text Solution
|
- If hat(i) denotes a unit vector along incident light ray hat( r) a uni...
Text Solution
|