A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
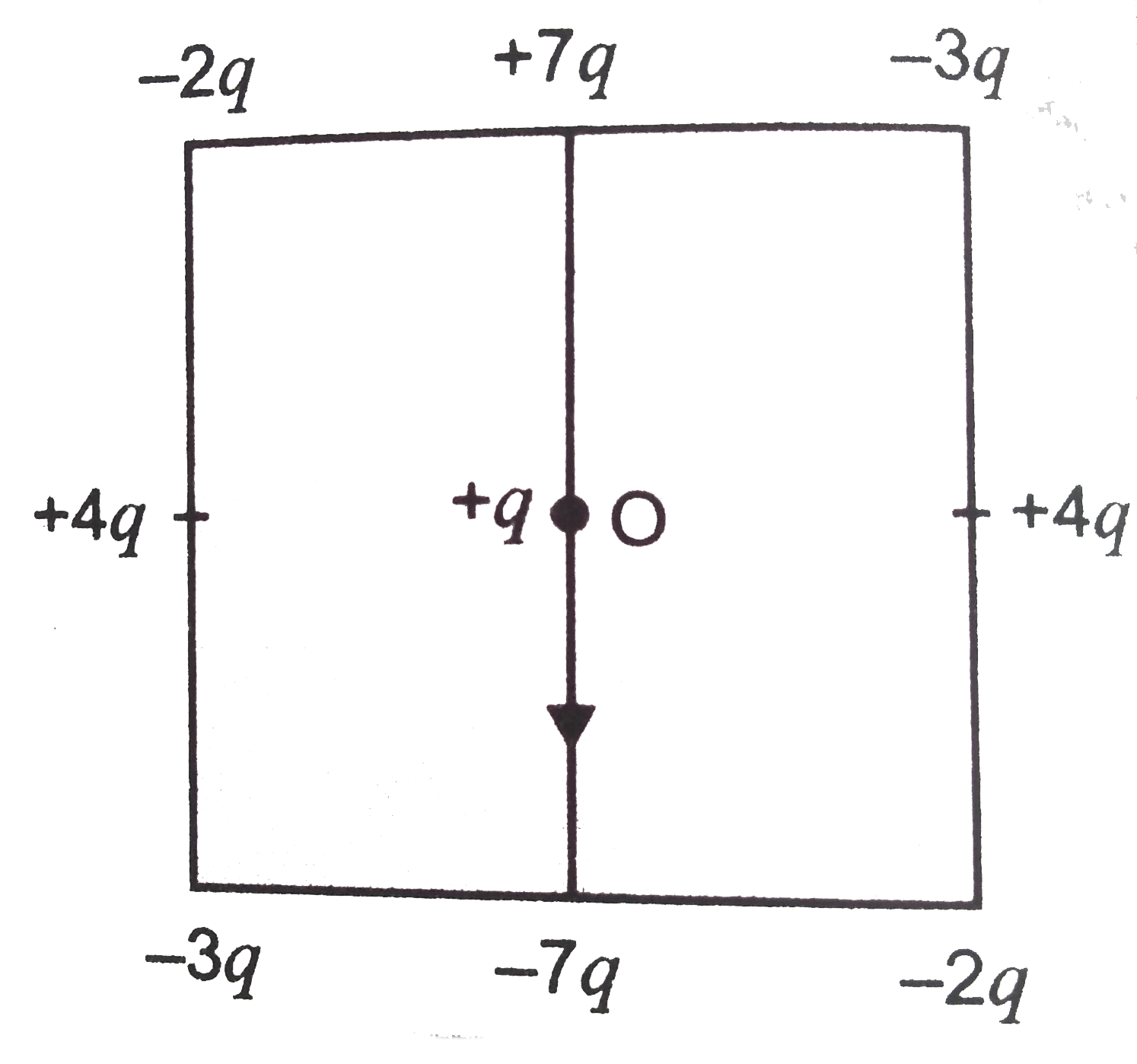
- A particle carrying charge + q is held at the center of a squar...
Text Solution
|
- Four positive charges (2sqrt2-1)Q are arranged at the four corners of ...
Text Solution
|
- Point charge are placed at the verticas of a squre of side a as shown ...
Text Solution
|
- A particle carrying charge + q is held at the center of a square of ea...
Text Solution
|
- Four equal charges each 16 muC are placed on four corners of a square ...
Text Solution
|
- Four charge Q, q, Q and q are kept at the four corners of a square as ...
Text Solution
|
- Consider the charge q, q and -q placed at the vertices of an equilater...
Text Solution
|
- The work which is required to be done to make an arrangement of four p...
Text Solution
|
- Four charge particles of chagres -q,-q,-q and 3q are placed at the ...
Text Solution
|