Text Solution
Verified by Experts
Recommended Questions
- An inclinded plane making an angle of 30^(@) with the horizontal elec...
Text Solution
|
- A block of mass 5.0kg slides down from the top of an inclined plane of...
Text Solution
|
- An inclinded plane making an angle of 30^(@) with the horizontal elect...
Text Solution
|
- A particle sides down from rest on an inclined plane of angle theta wi...
Text Solution
|
- A smooth inclined plane is inclined at an angle theta with the horizon...
Text Solution
|
- A particle is projected from horizontal making an angle of 53^(@) with...
Text Solution
|
- An inclined plane of length 5.60 m making an angle of 45^(@) with the ...
Text Solution
|
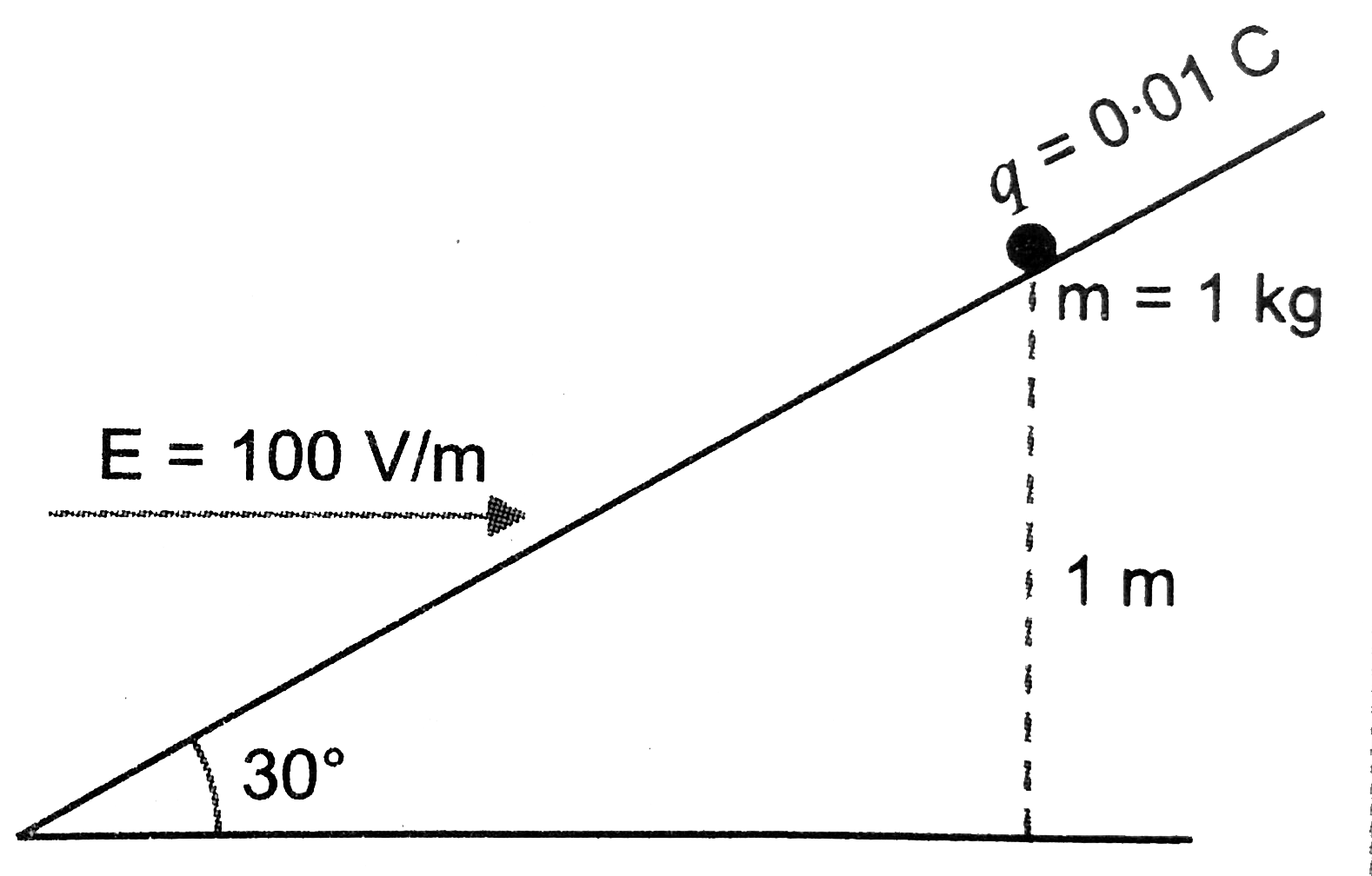
- A particles of mass 1kg and carrying positive charge 0.01C is sliding ...
Text Solution
|
- A particle of mass 1kg and carrying 0.01C is at rest on an inclined pl...
Text Solution
|