According to early model of an atom,the atom is considered it to have a positively charged point nucleus of charge `Ze` surrounded by a uniform density of negative charge up to a radius `R`. The atom as a whole is neutral. The electric field at a distance`r` from the nucleus is `(r lt R)`

Explanation

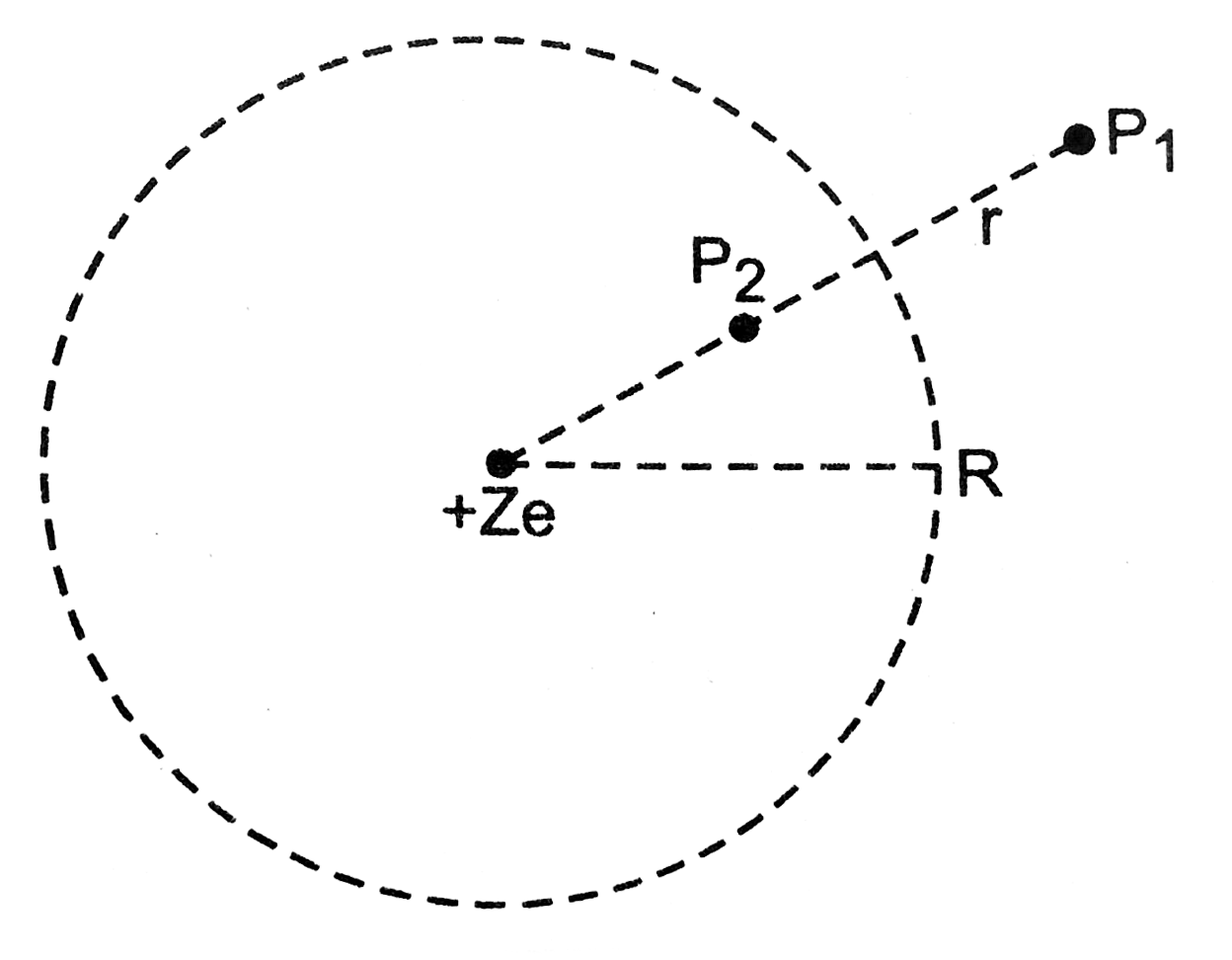
The charge distribution for this model of atom is shown in Fig.
Charge on nucleas `= +Ze` , As atom is neutral, total negative charge `= -Ze`
`:.` Negative charge density, `p = (charg e)/(Volume)`

`p = (-Ze)/((4)/(3) 4pi R^(3)) = (-3Ze)/(4pi R^(3))` ...(i)
Imagine a Gaussian surface - which is a spherical surface of radius r with center at the nucleaus (not shown).
According to Gauss's theorem in electrostatics.
`phi = E(r)xx4pi r^(2) = (q)/(in_(0))` ...(ii)
(i) When point `P_(1)` is outside,
i.e., `r gt R, q = Ze - Ze = 0 :. E(r) = 0`.
(ii) When point `P_(2)` is inside, i.e., `r gt R`, Charge enclosed by Gaussain surface.
`q' = Ze + (4pi r^(3))/(3) p = Ze - Ze (r^(3))/(R^(3))` ...using (i)
From (ii), `E (r) = (q')/(4pi in_(0) r^(2)) = (Ze-Ze r^(3) // R^(3))/(4pi in_(0) r^(2))`
`= (Ze)/(4pi in_(0)) ((1)/(r^(2)) - (r)/(R^(3)))`