Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
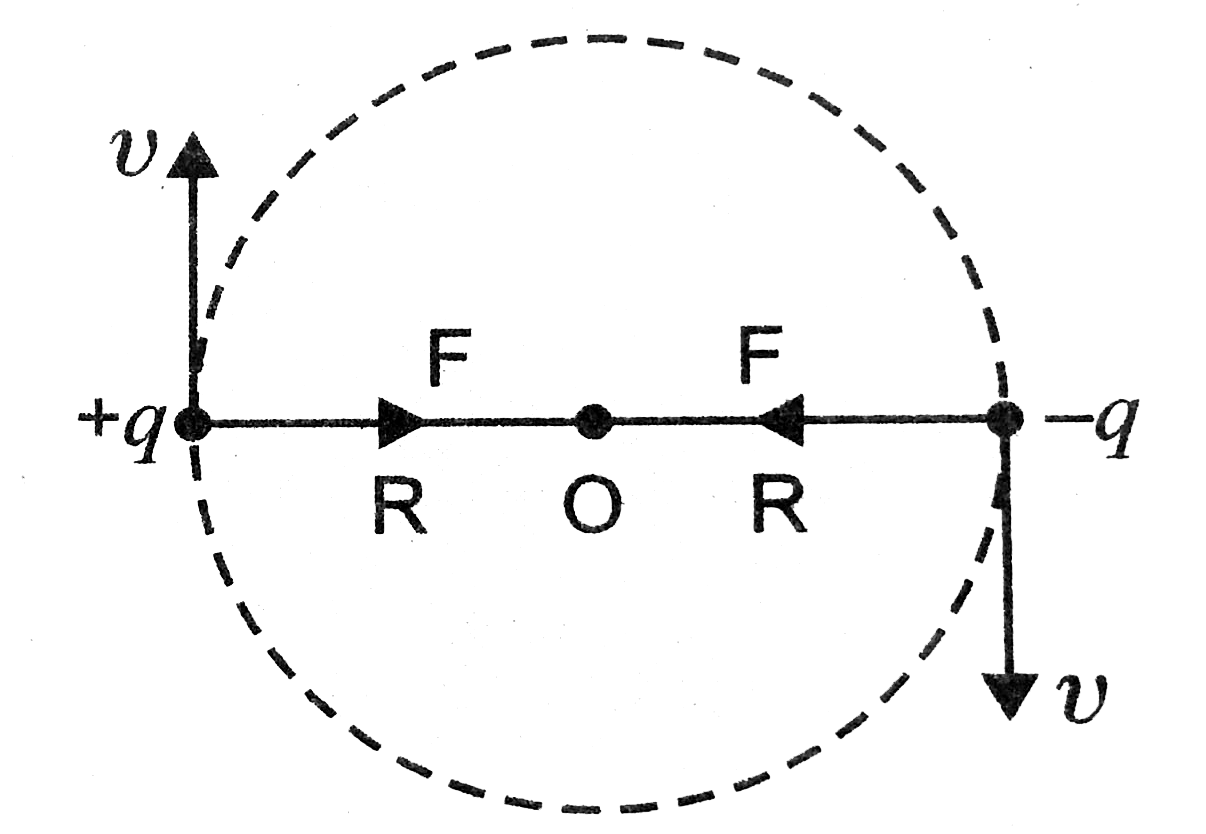
- Two charges +q and -q, each of mass m, are revoloving in a circle of ...
Text Solution
|
- For the eletrostatic charge system as shown in (Fig. 3.121), find . a....
Text Solution
|
- Charges -q , Q, and -q are placed at an equal distance on a straight l...
Text Solution
|
- What do you understand by electrostatic potential energy ? Find an ex...
Text Solution
|
- Two charges +q and -q, each of mass m, are revoloving in a circle of ...
Text Solution
|
- Eight point charges , each q , are placed on the vertices of a cube of...
Text Solution
|
- Two equal charges of magnitude Q each are placed at a distance d apart...
Text Solution
|
- If Q charge is given to a sphere of radius R, the energy of the system...
Text Solution
|
- Two charges +q and -q, each of mass m, are revoloving in a circle of ...
Text Solution
|