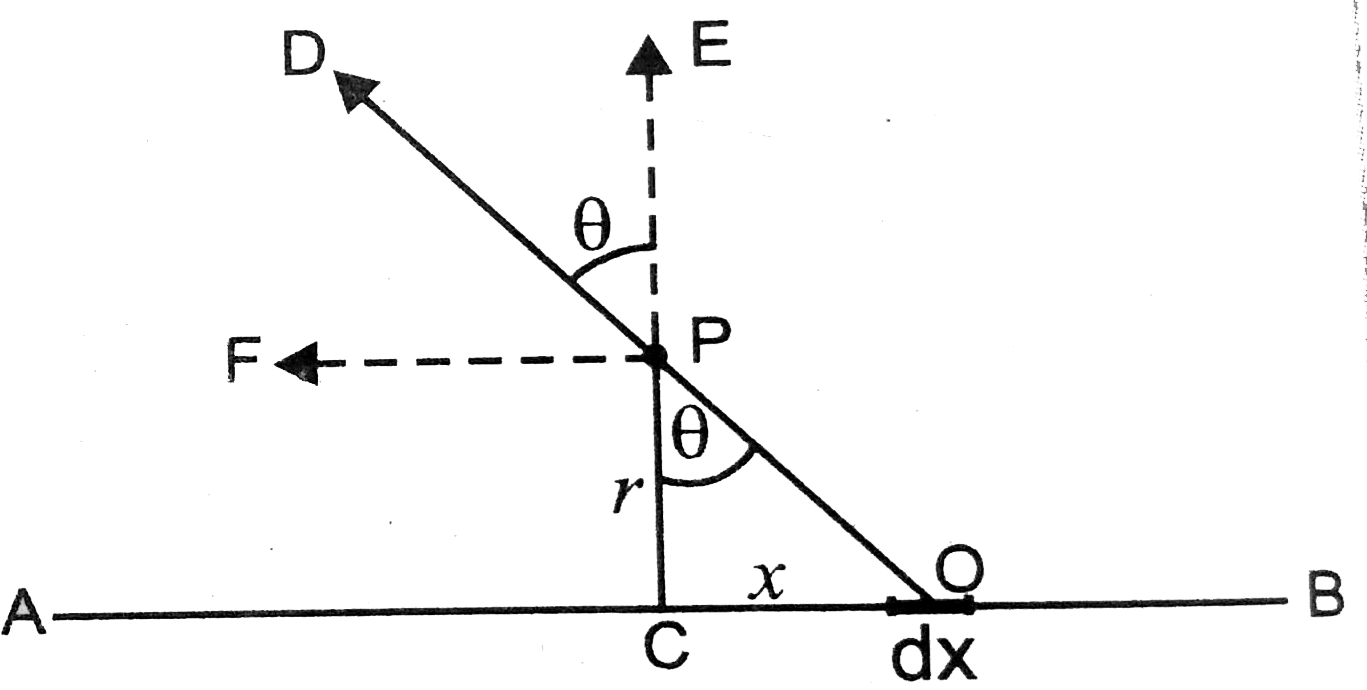
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Obtain the formula for the electric field due to a long thin wire of ...
Text Solution
|
- Obtain the formula for the electric field due to a long thin wire of ...
Text Solution
|
- The electric field intensity due to a thin infinity long straight wire...
Text Solution
|
- गाउसीन नियम का उपयोग किये बिना एकसमान रैखिक आवेश घनत्व lambda के लंबे ...
Text Solution
|
- गोस नियम का उपयोग किये बिना किसी एक्शमन रेखिक आवेश घनत्व lambda क...
Text Solution
|
- गॉस के नियम द्वारा रेखीय आवेश के कारण विद्युत् क्षेत्र की तीव्रता ज्ञा...
Text Solution
|
- Obtain the formula for the electric field due to a long thin wire of u...
Text Solution
|
- गाउस नियम का उपयोग किए बिना किइस एकसमान रैखिक आवेश घनत्व lamda के लम्...
Text Solution
|
- Obtain the formula for the electric field due to a long thin wire of u...
Text Solution
|