Consider a sphere of radius R with charge density distributed as `rho (R) = kr` for `r le R and = 0` for `r gt R`.
(a) Find the electric field at all points r.
(b) suppose the total charge on the sphere is 2e, where e is the electron charge. Where can two protons be embedded such that the force on each of them is zero. Assume that the introduction of the proton does not alter the negative charge distribution.

Explanation

The given charge density distribution of the sphere fo radius R is
`rho (r ) = k r` for `r le R`
`= 0` for `r gt R`
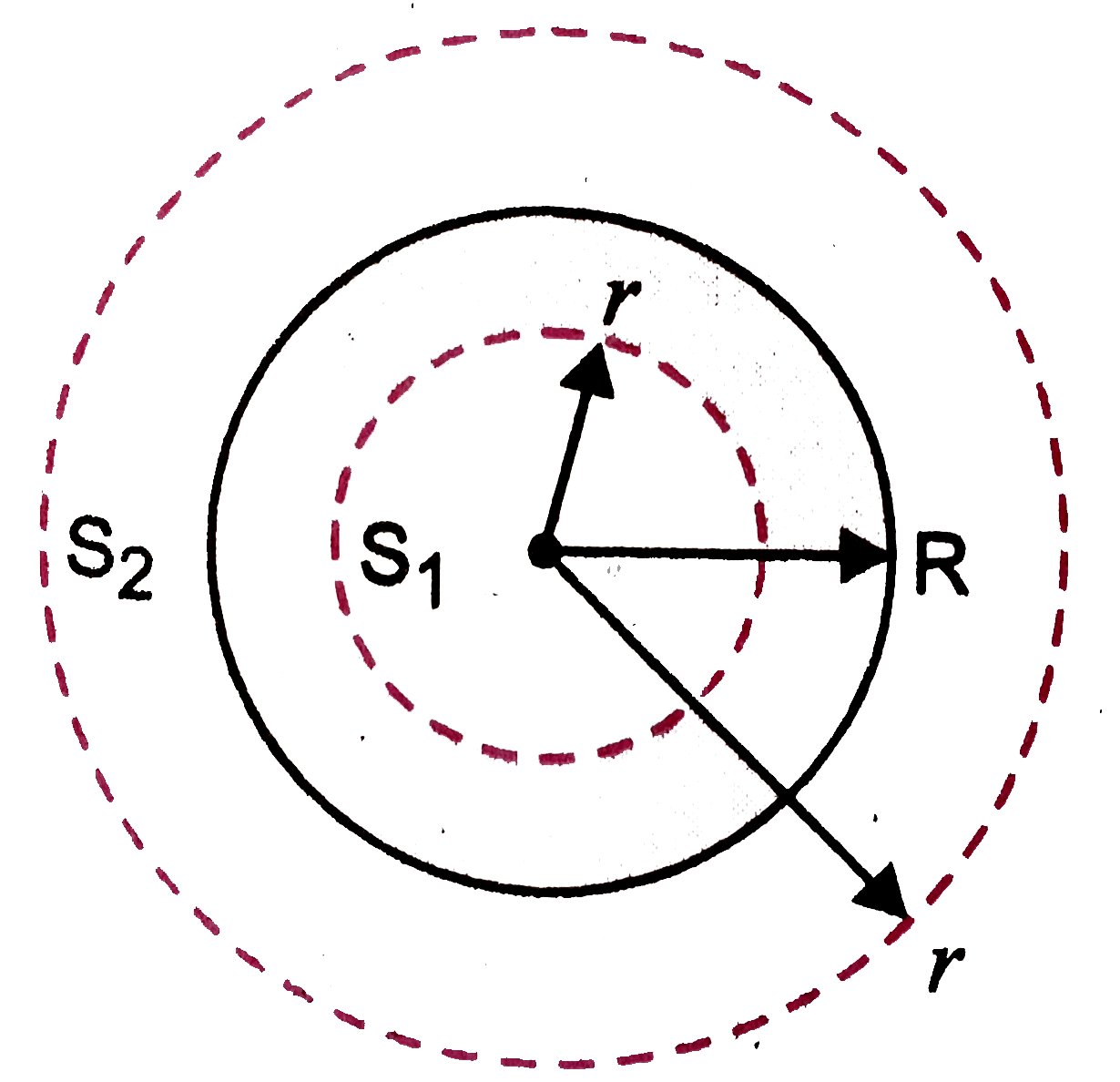
The electric field is obviously radial, as shown in Fig.
For points `r lt R`
Let us consider a spherical Gaussian surface `S_(1)` of radius r. Then on the surface,
`oint vec(E). vec(ds) = (1)/(in_(0)) int rho dV`
As `V = (4)/(3) pi r^(3), dV = (4)/(3) pi 3, r^(2) dr = 4pi r^(2) dr and rho(r) = kr :. oint vec(E). vec(ds) = (1)/(in_(0)) 4pi k int_(0)^(r) r r^(2) dr`
`(E) 4pi r^(2) = (4pi k)/(in_(0)) (r^(4))/(4)`
or `E = (1)/(4 in_(0)) kr^(2)` ...(i)
The direction of `vec(E)` is radially outwards (for positive charge density)
For points `r gt R`, let us consider a sphericall Gaussian surface `S_(2)` of radius r. Then on the surface, when `r = R`
`oint vec(E). vec(ds) = (1)/(in_(0)) int rho. dV`
`E(4pi r^(2)) = (4pi k)/(in_(0)) int_(0)^(R) r^(3) dr = (4pi k)/(in_(0)) dr = (4pi k)/(in_(0)) (R^(4))/(4)`
or `E = (k)/(4 in_(0)) (R^(4))/(r^(2))`
The direction of `vec(E)` is radially outwards (for positive charge density).
(b) From symmetry, we find that the two protons must be on the opposite sides of the center, along a diameter of the sphere as shown in Fig. Proceeding as above, charge on the sphere.
`q = int_(0)^(R) rho dV = int_(0)^(R) (kr) 4pi r^(2) dr = 4pi k (R^(4))/(4) = 2e`
`:. k = (2e)/(pi R^(4))` ....(iii)
If protons 1 and 2 are embedded at distance r from the center of the sphere as shown , then attractive force on proton 1 due to charge distribution is
`F_(1) = -e E = -e (kr^(2))/(4 in_(0))` ....using (i)
Repulsive force on proton 1 due to proton 1 due to proton 2 is `F_(2) = (e^(2))/(4pi in_(0) (2r)^(2))`
Net force on proton 1 `F = F_(1) + F_(2) = -e (kr^(2))/(4in_(0)) + (e^(2))/(16pi in_(0) r^(2))`
Using (iii), `F = [- (er^(2))/(4in_(0)) (2e)/(pi R^(4)) + (e^(2))/(16pi in_(0) r^(4)) ]`
This net force on proton 1 will be zero, when `(e r^(2). 2e)/(4 in_(0)) = (e^(2))/(16 pi in_(0) r^(2)) or r^(4) = (R^(4))/(8) or r = (R)/((8)^(1//4))`
This is the distance of each of the two protons from the center of the sphere.