Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- (a) In a quark model of elementary particles, a neutron is made of one...
Text Solution
|
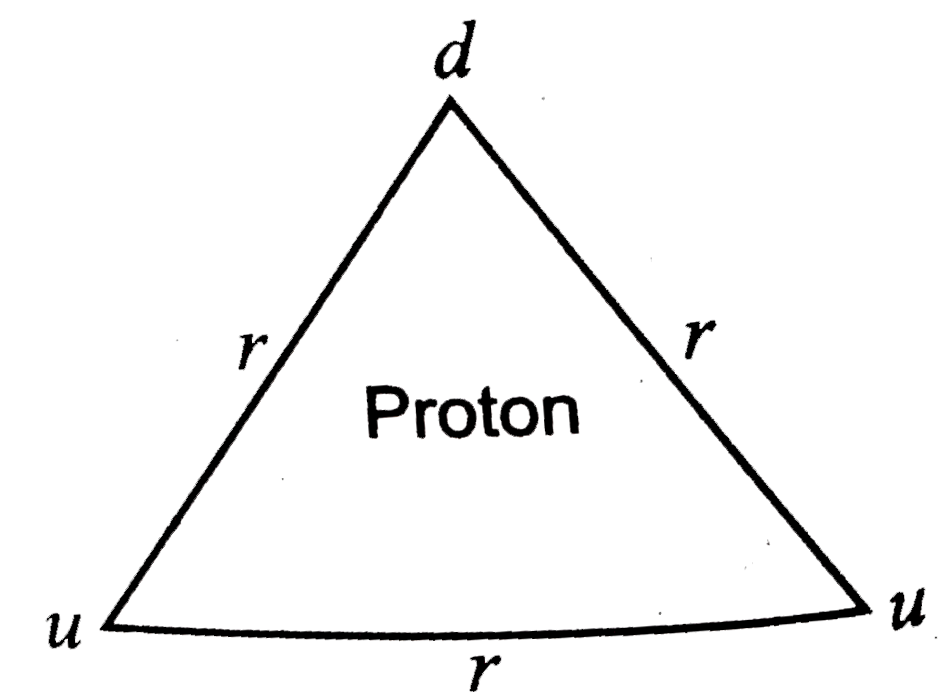
- It is now believed that protons and neutrons (which consitude nuclel o...
Text Solution
|
- (a) In a quark model of elementary particles, a neutron is made of one...
Text Solution
|
- अब ऐसा विश्वास किया जाता है की स्वयं प्रोटॉन एवं न्यूट्रॉन (जो सामान्...
Text Solution
|
- अब ऐसा विश्वास किया जाता है की सवंय प्रोटोन पर न्यूट्रॉन (जो सामान्य द...
Text Solution
|
- न्यूट्रॉन एक अनावेशित परंतु 9.66xx10^(-27) Am^(2) का z - अक्षीय चुंबक...
Text Solution
|
- It is now believed that protons and neutrons (which constitute nuclei ...
Text Solution
|
- It is now believed that protons and neutrons ( which constitute nucleI...
Text Solution
|
- मूल कणों के क्वार्क मॉडल में एक प्रोटॉन, दो “अप " क्वार्क, प्रत्येक का...
Text Solution
|