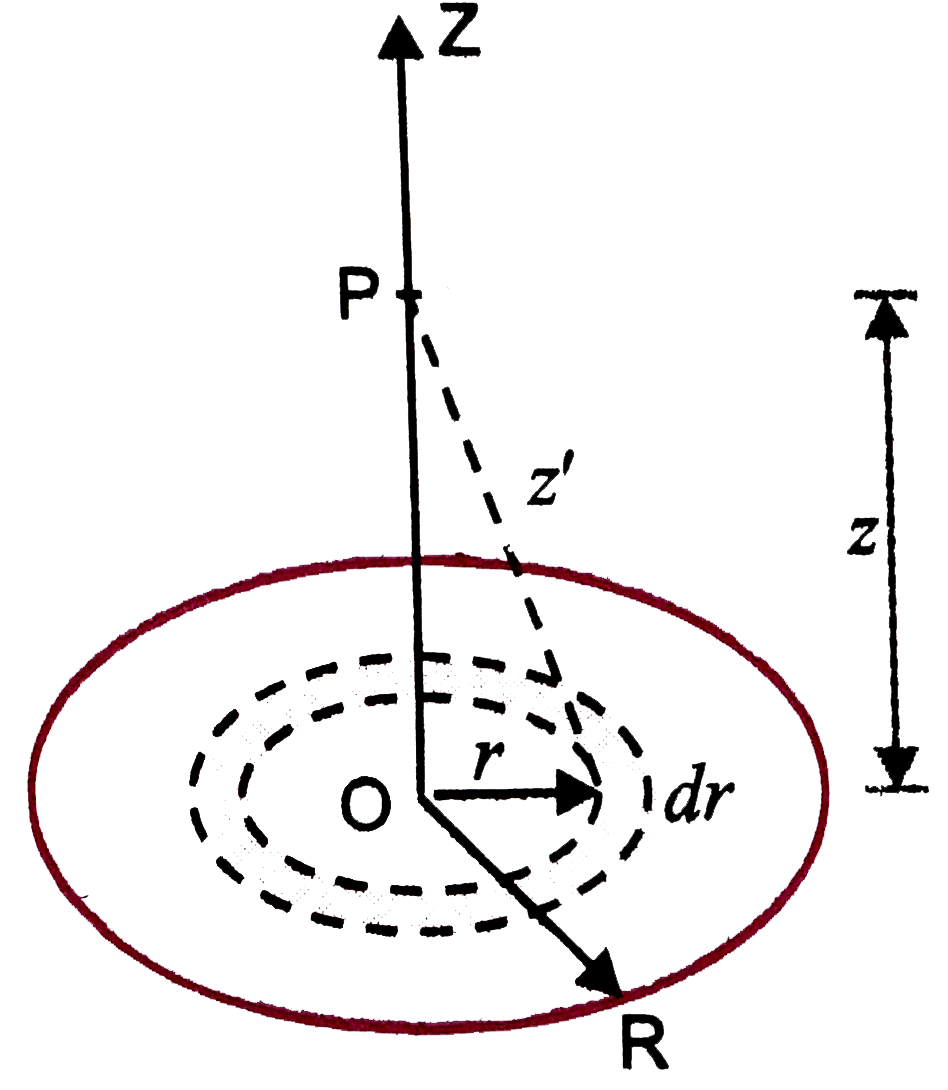Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Calculate potential on the axis of a disc of radius R due to a charge ...
Text Solution
|
- A charge q is uniformly distributed on a non-conducting disc of radius...
Text Solution
|
- Charge q is uniformly distributed on a disc of radius r. If the disc i...
Text Solution
|
- Calculate potential on the axis of a ring due to charge Q uniformly ...
Text Solution
|
- Calculate potential on the axis of a disc of radius R due to a charge ...
Text Solution
|
- Find the potential varphi at the edge of a thin disc of radius R carry...
Text Solution
|
- A plastic disc of radius 'R' has a charge 'q' uniformly distributed ov...
Text Solution
|
- A flat disc of radius R charged uniformly on its surface at a surface ...
Text Solution
|
- A thin disc of radius R has charge Q distributed uniformly on its surf...
Text Solution
|