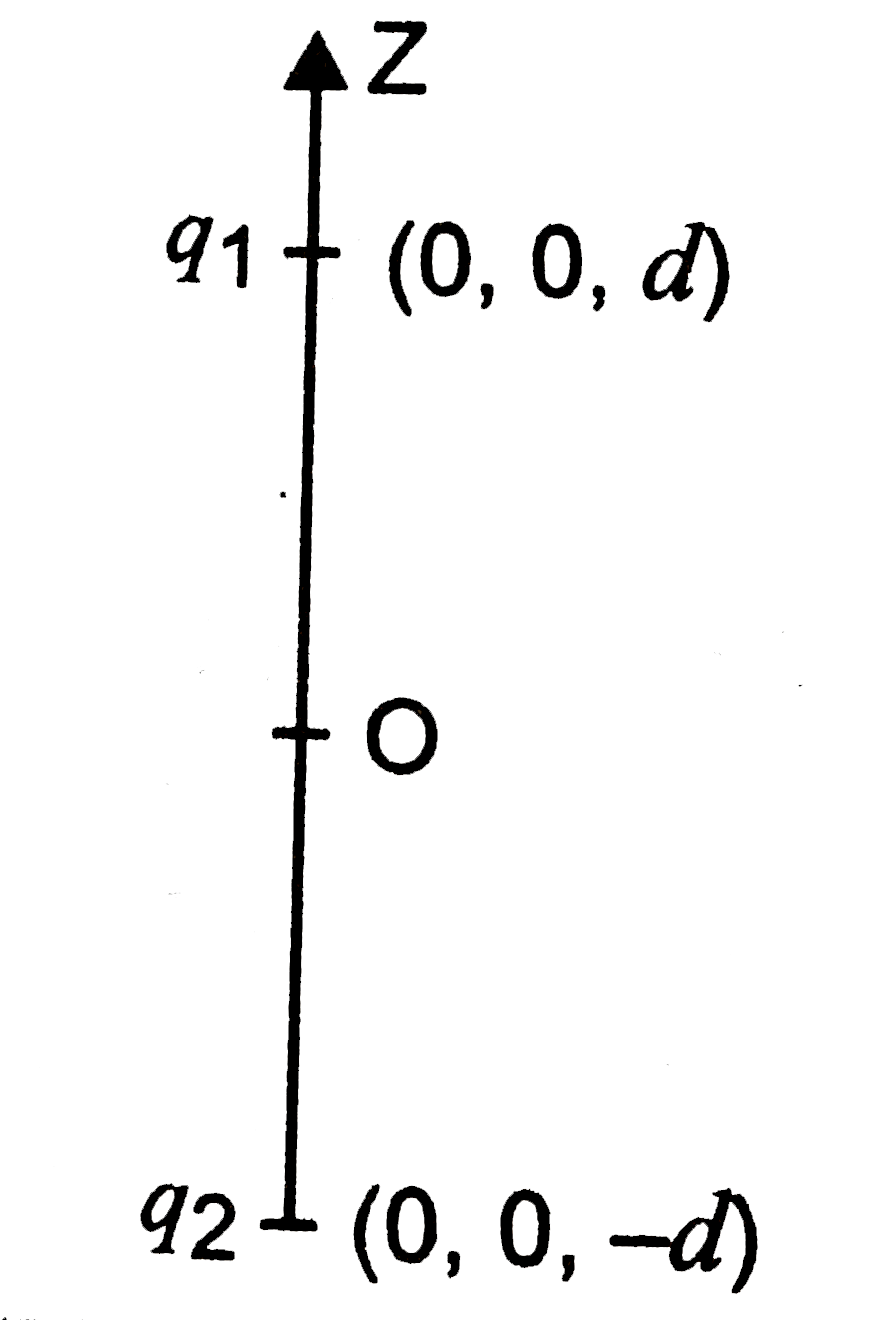Text Solution
Verified by Experts
Topper's Solved these Questions
ELECTROSTATICS
PRADEEP|Exercise VALUE BASED QUESTIONS|7 VideosELECTROSTATICS
PRADEEP|Exercise Exercise|414 VideosELECTROSTATICS
PRADEEP|Exercise ADDITIONAL QUESTIONS|2 VideosELECTRONIC DEVICES
PRADEEP|Exercise Fill in the Blanks|1 VideosMAGNETIC EFFECT OF CURRENT AND MAGNETISM
PRADEEP|Exercise Competition Focus (Multiple Choice Questions)|2 Videos
Similar Questions
Explore conceptually related problems
PRADEEP-ELECTROSTATICS-LONG ANSWER QUESTIONS
- Derive an expression for electric field intensity at a point due to po...
Text Solution
|
- (i) If two similar large plates, each of area A having surface charge ...
Text Solution
|
- In 1959, Lytteton and Bondi suggest that the expansion of the Universe...
Text Solution
|
- Two fixed, identical conducting plates (alpha and beta), each of surf...
Text Solution
|
- Three is another useful system of units, besides the SI/mksA system, c...
Text Solution
|
- Find the equatio of the equipotentials for an infinite cylinder of rad...
Text Solution
|
- Two charges q(1) and q(2) are placed at (0,0,d) and (0,0,-d) respectiv...
Text Solution
|
- Two charges -q each are separated by dsitance 2d. A third charge +q i...
Text Solution
|