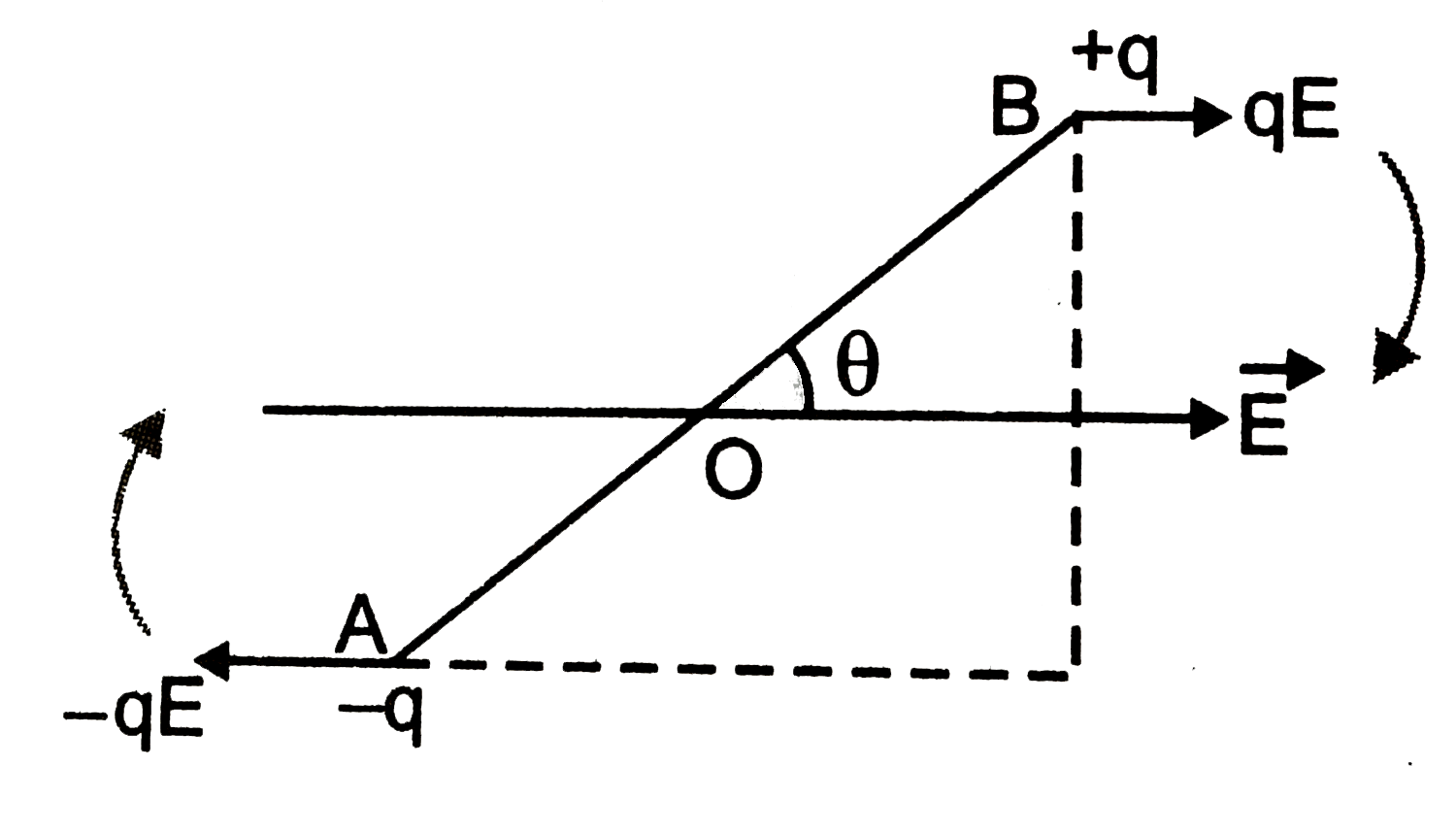
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A point particle of mass M is attached to one end of a massless rigid ...
Text Solution
|
- A point particle of mass M is attached to one end of a massless rigid ...
Text Solution
|
- A particle is attached to an end of a rigid rod. The other end of the ...
Text Solution
|
- A particle of mass m is attached to one end of missless rigid non-cond...
Text Solution
|
- A point mass M is attached to one end of a masslesa rigid non-conducti...
Text Solution
|
- A point mass M is attached to one end of a masslesa rigid non-conducti...
Text Solution
|
- A point mass M is attached to one end of a masslesa rigid non-conducti...
Text Solution
|
- A particle is attached to the lower end of a uniform rod which is hing...
Text Solution
|
- A uniform rod of mass m and length L is hinged at one of its end with ...
Text Solution
|