Home
Class 12
PHYSICS
Two conductors of conductnaces G(1) and ...

Two conductors of conductnaces `G_(1)` and `G_(2)` are connected in series. They are connected in parallel to another conductor of conductance `G_(3)`. Determine their equivalent conductance.

Text Solution

Verified by Experts

Let `R_(1),R_(2)` and `R_(3)` be the resistances of conductors of conductances `G_(1),G_(2)` and `G_(3)` respectively.
Here `R_(1)=1/G_(1),R_(2)=1/G_(2),R_(3)=1/G_(3)` The effective resistance between A to B is

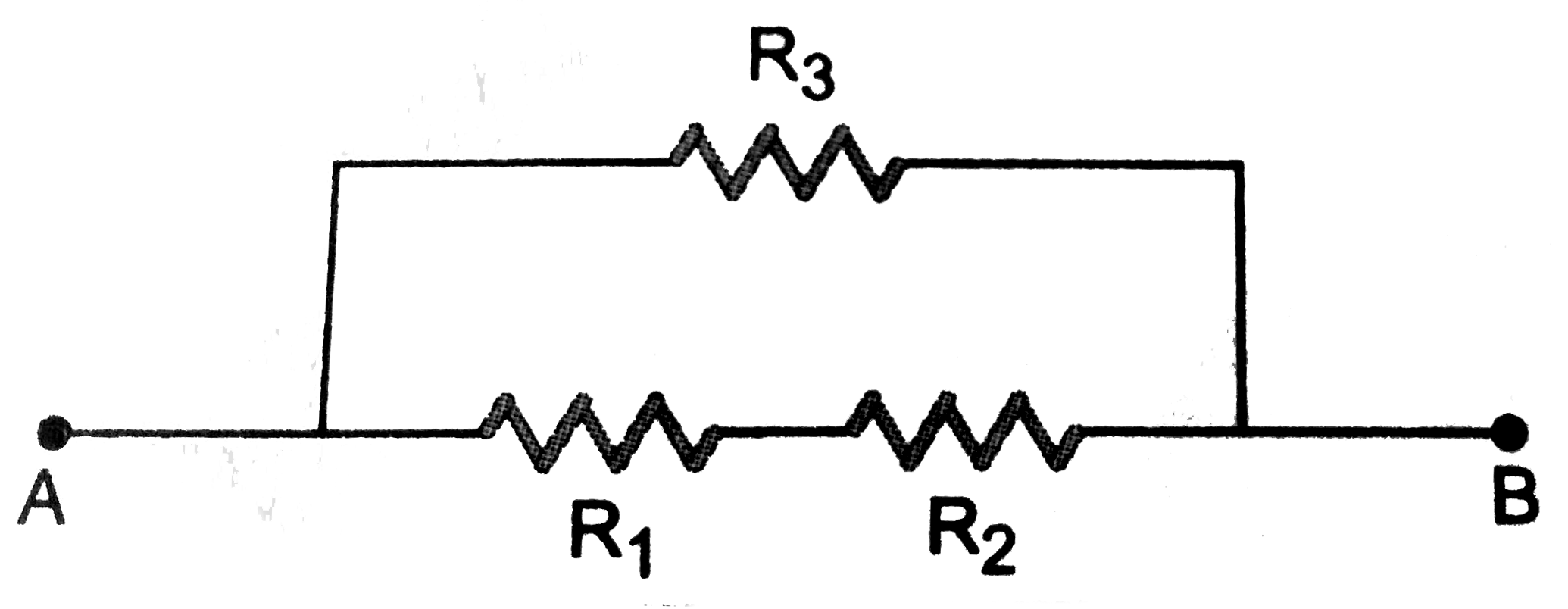
`R=(R_(3) xx (R_(1) +R_(2)))/(R_(3)+(R_(1) +R_(2)))`
`:.` Effective conductance,
`G=1/R = (R_(3) +(R_(1) +R_(2)))/(R_(3)xx(R_(1) +R_(2)))`
`:. G =(1/(G^(3)) + 1/(G_(1)) +1/(G_(2)))/(1/(G_(3))xx(1/(G_(1)) +1/(G_(2))))`
`(G_(1)G_(2) +G_(2)G_(3) +G_(1)G_(3))/((G_(2) +G_(1)))`
Promotional Banner

Topper's Solved these Questions

  • CURRENT ELECTRICITY

    PRADEEP|Exercise Conceptual Problems|3 Videos

  • CURRENT ELECTRICITY

    PRADEEP|Exercise Very short Q/A|7 Videos

  • COMMUNICATION SYSTEMS

    PRADEEP|Exercise MODEL TEST PAPER-2|9 Videos

  • DUAL NATURE OF RADIATION AND MATTER

    PRADEEP|Exercise Exercise|191 Videos

Similar Questions

Explore conceptually related problems

Three conductors of conductances G_(1), G_(2) " and " G_(3) are connected in series. Find their equivalent conductance.

Two identical metal wires of thermal conductivities K_(1) and K_(2) respectively are connected in series. The effective thermal conductivity of the combination is :

Two conductors of resistance R_(1) (50 +- 2) ohm and R_(2) = (100 +- 4) ohm are connected in (a) series and (b) parallel. Find the equivalent resistance.

Three identical condensers are connected together in four different ways. First all of them are connected in series and the equivalent capacity is C_(1) . Next all of them are connected in parallel and the equivalent capacity is C_(2) . Next two of them are connected in series and the third one connected in parallel to the combination and the equivalent capacity is C_(3) . Next two of them are connected in parallel and the third one connected in series with the combination and the equivalent capacity is C_(4) . Which of the following is correct ascending order of yhe equivalent capacities ?

Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K_1 and K_2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod. Statement II: For two cylindrical rods of identical size and different thermal conductivity K_1 and K_2 connected in series, the equivalent thermal conductivity K is given by (2)/(K)=(1)/(K_1)+(1)/(K_2)

Two conductors A and B given in previous problem are connected in parallel as shown in Fig. i. Determine the equivalent thermal resistance. ii. Determine the heat current in each rod.

Two small conductors A and B are given charges q_(1) and q_(2) respectively. Now they are placed inside a hollow metallic conductor C carrying a charge Q. If all the three conductors A, B and C are connected by a conducting wire as shown, the charges on A,B and C will be respectively :

There are two conductors of capacitance C and 2C are charged equally with charge +Q each and connected with a thin conducting wire and a switch as shown in figure. Find the final charges on the conductors after closing the switch.

Two identical capacitors are first connected in series and then in parallel. The ratio of equivalent capacitance is