In the circuit shown in figure-3.159 cells E,F,G and H are of EMF 2V, 1V,3V and 1V respevitly and their internal resitance are `2Omega,1Omega,3Omega` and `1Omega` respectively Calculate
(a) The potential difference between points B and D
(d) The potential difference across the terminals of the cell G and H.

Explanation

(i) The complete network has been with currents in the various arms.

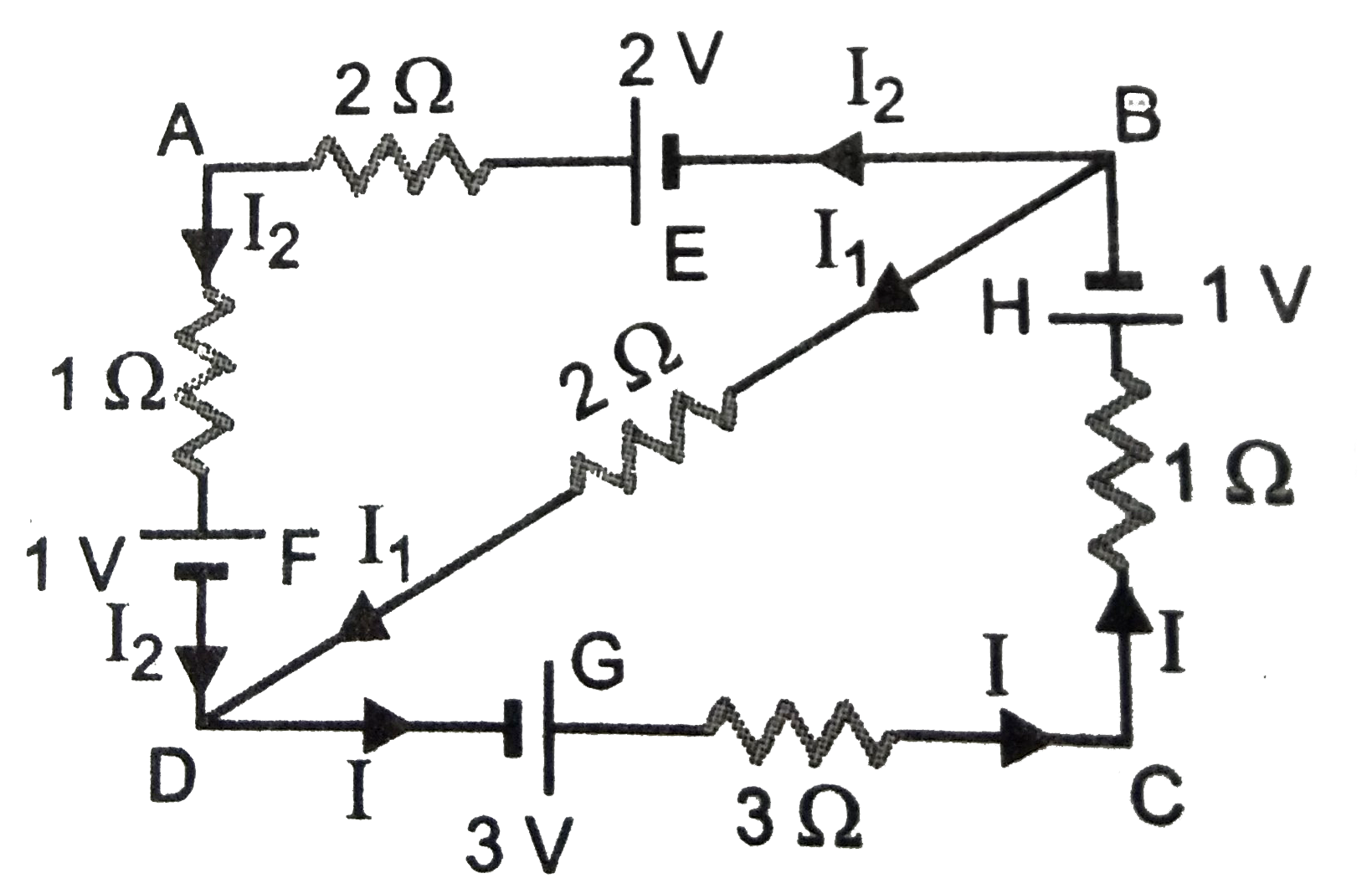
Applying Kirchhoff's first rule at junction B,
`I = I_(1) + I_(2)`
Applying Kirchoff's second rule to loop ABDA, we get
`-2 I_(2) + 2 I_(1) - 1 I_(2) = - 2+ 1`
or `2 I_(1) - 3I_(2)= -1`
For loop BCDB, we
` - 1 xx I - 3 xx I - 2 I_(1) = 1 - 3 = - 2`
or `2 = 4 I + 2 I_(1) = 4(I_(1) + I_(2))+2 I_(1)`
or ` 1 = 2(I_(1)+I_(2))+I_(1) +2I_(2)`
or `3 I_(2) + 2I_(2)=1`
On solving (i), (ii) and (iii), we get
`I_(1)=1/13 A, I_(2) = 5/13A and I=6/13A`
Pot. diff. between points B and D
`= I_(1) xx 2 = 1/13 xx 2 = 2/13V`
(ii) Pot. diff. across the treminals of G (giving current)
`V_(G)= epsilon - Ir = 3 - (6/13)xx = 1.615 V`
Pot. diff. across the terminals of H (receving current for charging)
`V_(H) = epsilon' + I r' = 1 + (6/13) xx 1 = 1.46V`