Let ABCDKLMN be the skeleton cube formed by joining twelve equal wires each of resistance r.
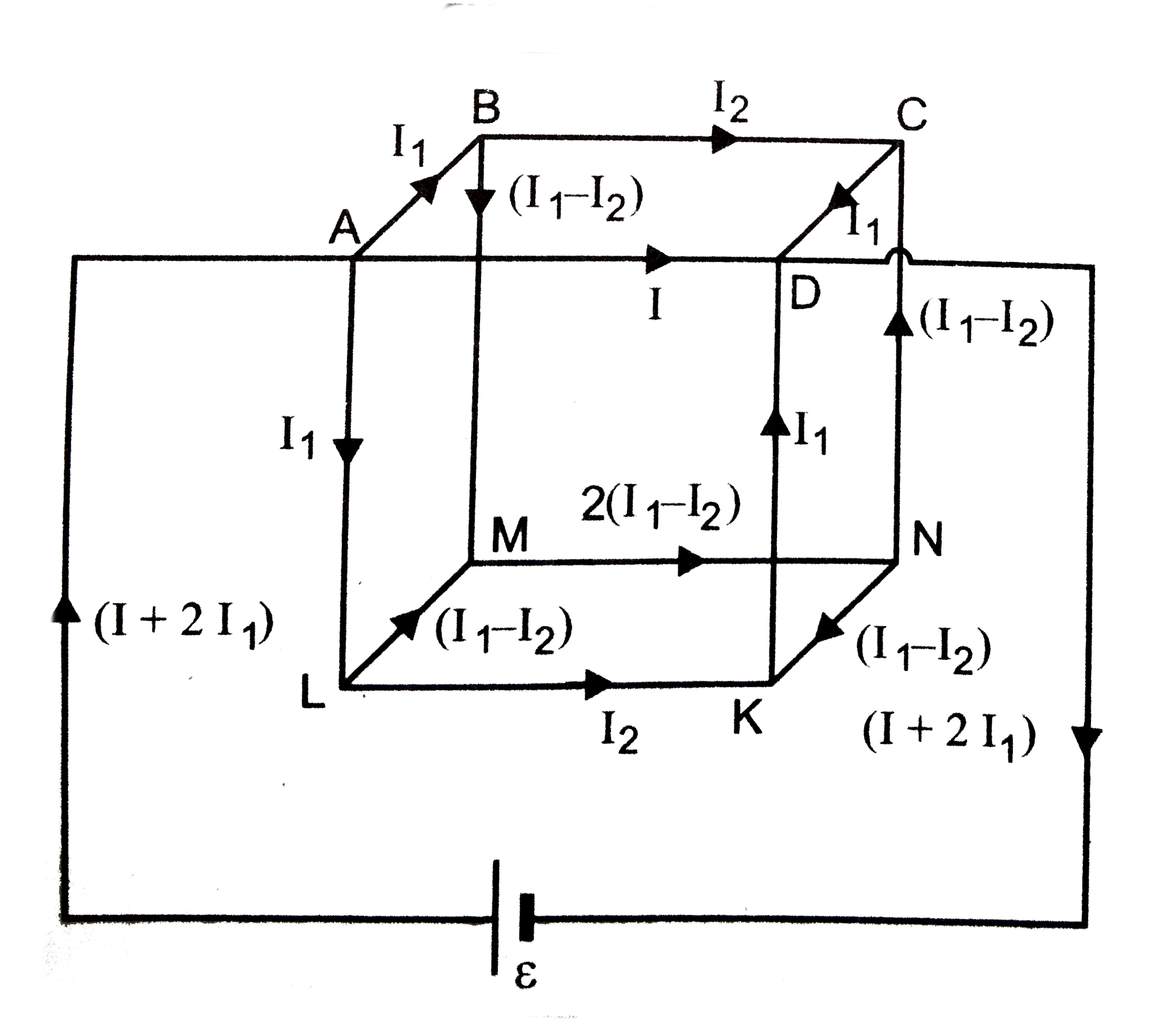
Let the current enter the cube at corner A and after passing through all twelve wires, let the current leave at D, other corner of the same edge of the cube.
For the sake of convenience, let us suppose that the total current is `(I + 2 I_(1))`. At A, this current is divided into three parts : I along AD and `I_(1)` each along AB and AL as the resistance along AB and AL are the same but along AD, it is different. At the points B and L, current is further divided into two unequal parts. The distribution of current in the various arms of skeleton cube is shown according to Kirchhoff's First rule. The current leaving the cube at D is again `(I + 2 I_(1))`. Applying Kirchhoff's Second rule to the closed meah ABCDA , we get
`I_(1)r + I_(2) r + I_(1)r-I r = 0`
or `2 I_(1) + I_(2) = I`
For closed mesh BCNMB ,
`I_(2) r - (I_(1)- I_(2)) r - 2 (I_(1)- I_(2)) r - (I_(1)-I_(2))r=0`
or `I_(2)r= 4 (I_(1) - I_(2))r`
or `I_(2) = 4 I_(1) - 4 I_(2)`
or `5 I_(2) = 4 I_(1) or I_(2) = 4/5 I_(1)`
From(i) , `I=2 I_(1) + 4/5 I_(1) = 14/5 I_(1)`
For closed mesh AD`epsilon`A, `Ir= epsilon`
Where `epsilon` is the emf of the cell of negligible internal resistance.
If R is the total resistance between the two corners of the same edge of the cube, then applying Kirchhoff's second rule for the closed mesh AD`epsilon` A, we get,
`(I + 2I_(1))R=epsilon or (14/5 I_(1)+2 I_(1))R=epsilon`
or `24/5 I_(1) R= epsilon`
From (iii) and (iv), `14/5 I_(1) r = epsilon`
From (v) and (vi),
`24/5 I_(1)R = 14/5 I_(1)r or R=14/24 r = 7/12r`