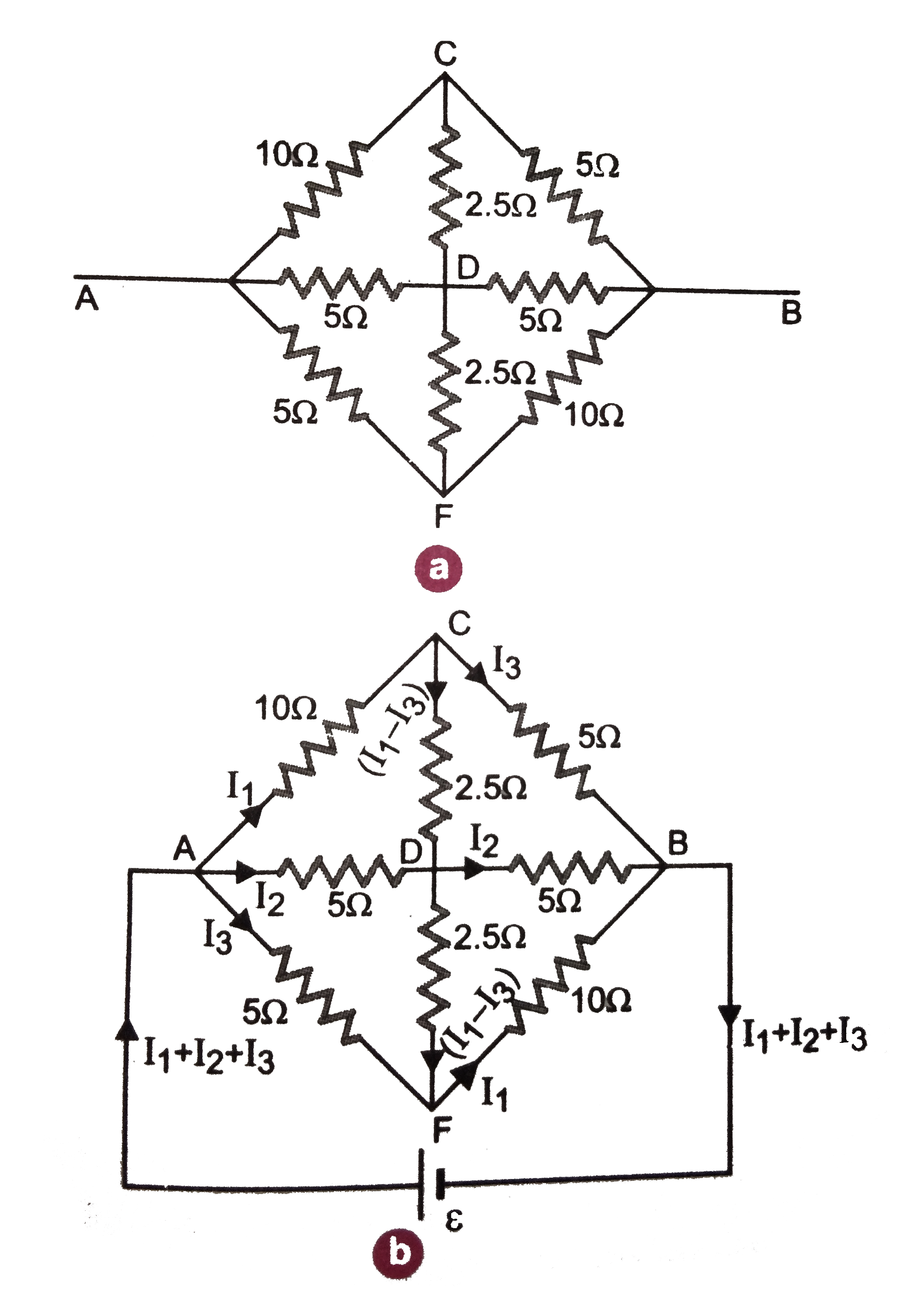
Connect a battery of emf `epsilon` between A and B. Let the currents `(I_(1) + I_(2) +I_(3))` enter the network at point A. The same current leaves the network at B. Let the currents through AC, AB and AF be `I_(1), I_(2) and I_(3)` respectively. Similar will be the distrbution of current at B. The current `(I_(1) + I_(2) +I_(3))` leaving at B is composed of `I_(1)` from FB, `I_(2)` from DB and `I_(3)` from CB.
According to Kirchoff's second law, in a closed circuit B`epsilon`ADB,
`epsilon = 5 I_(2) + 5 I_(2) = 10 I_(2)`
If R is the resistance of network between A and B, then
`epsilon = (I_(1) + I_(2) +I_(3))R`
From (i) and (ii),
`(I_(1) +I_(2)+I_(3)) R = 10 I_(2)`
In the closed circuit ACDA,
`10 I_(1) + 2.5 (I_(1) - I_(3)) - 5 I_(2) = 0`
or `12.5 I_(1) - 5 I_(2) - 2.5 I_(3)=0`
or `5 I_(1) - 2 I_(2) - I_(3) = 0`
In the closed circuit CBDC,
`5 I_(3) - 5 I_(2) - 2.5 (I_(1) -I_(3))=0`
or ` - 2.5 I_(1) - 5 I_(2) + 7.5 I_(3)=0`
or `-I_(1) - 2 I_(2) + 3I_(3)=0`
From (iv) and (v),
`5 I_(1) - I_(2) - I_(3) = - I_(1) - 2 I_(2)+ 3I_(3)`
or ` 6 I_(1) = 4I_(3) or I_(1) =4/6 I_(3)=2/3 I_(3)`
In the clsoed circuit ADFA,
`5 I_(2) + 2.5 (I_(1)- I_(3)) - 5 I_(3)=0`
or `2.5 I_(1) + 5 I_(2)-7.5I_(3)=0`
or `I_(1) + 2I_(2) - 3 I_(3) =0`
or `I_(1) + 2 I_(2) - 3I_(3)=0`
or `2 I_(3) + 6I_(2) - 9I_(3) = 0 or 6 I_(2) = 7 I_(3)`
or `I_(3) = 6/7 I_(2)`
From (vi), `I_(1) = 2/3 xx 6/7 I_(2) =4/7 I_(2)`
Putting values in (iii), we get
`(4/7 I_(2) + I_(2) + 6/7 I_(2)) R = 10 I_(2)`
or `17/7 R = 10 or R = (10 xx 7)/17 = 4.1 Omega`