What amount of heat will be generated in a coil of resistance `R` due to a charge q passing through it if the current in the coil
a. decreases down to zero uniformly during a time interval `t_0`?
b. decrases down to zero having its value every `t_0` seconds?

Explanation

As current in coil decreases uniformly with time, therefore the variation of current I and time t is straight line as shown in figure.
The slope of this straight line, `m = - I_(0)/t_(0)`. Since the current is a function of time, can be written as
`I = - (I_(0)/t_(0)) t + I_(0)`....(i) `[because y =mx +c)]`

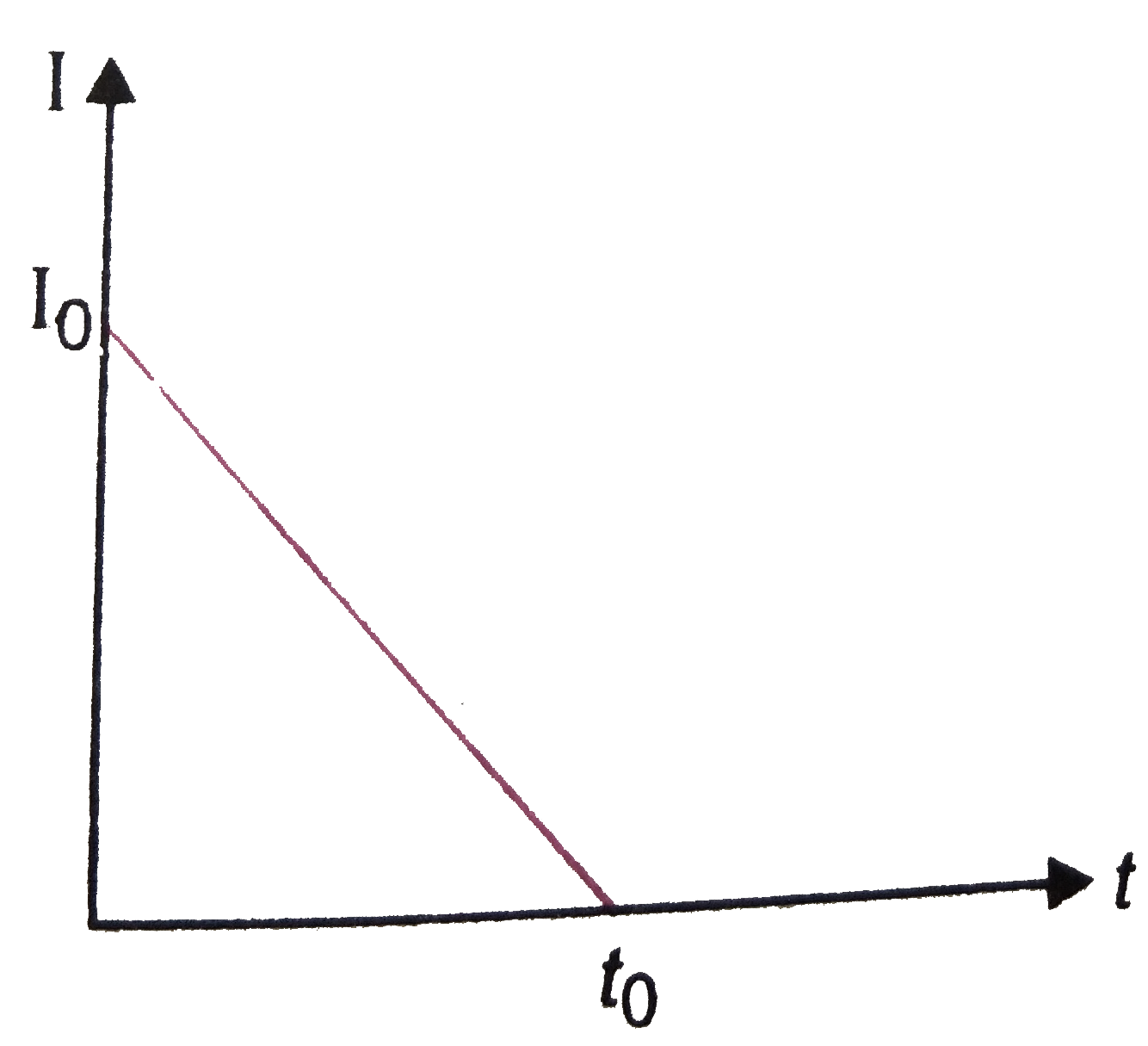
The area under I-t graph gives the flow of charge q. Therefore,
`q = 1/2 (I_(0) xx t_(0)) or I_(0) = (2q)/t_(0)`
Putting this value in (i), we get
`I = - ((2q//t_(0)))/t_(0) t + (2q)/t_(0) or I = ((2q)/t_(0) - (2qt)/t_(0)^(2))`
Heat produced in coil in a time interval dt is
`dH=I^(2)Rdt=((2q)/(t_(0))-(2qt)/(t_(0)^(2)))^(2)Rdt`
Total heat produced is
`H= underset(0)overset(t_(0))(int)((2q)/(t_(0))-(2qt)/(t_(0)^(2)))^(2)Rdt=(4)/(3)xx(q^(2)R)/(t_(0))`