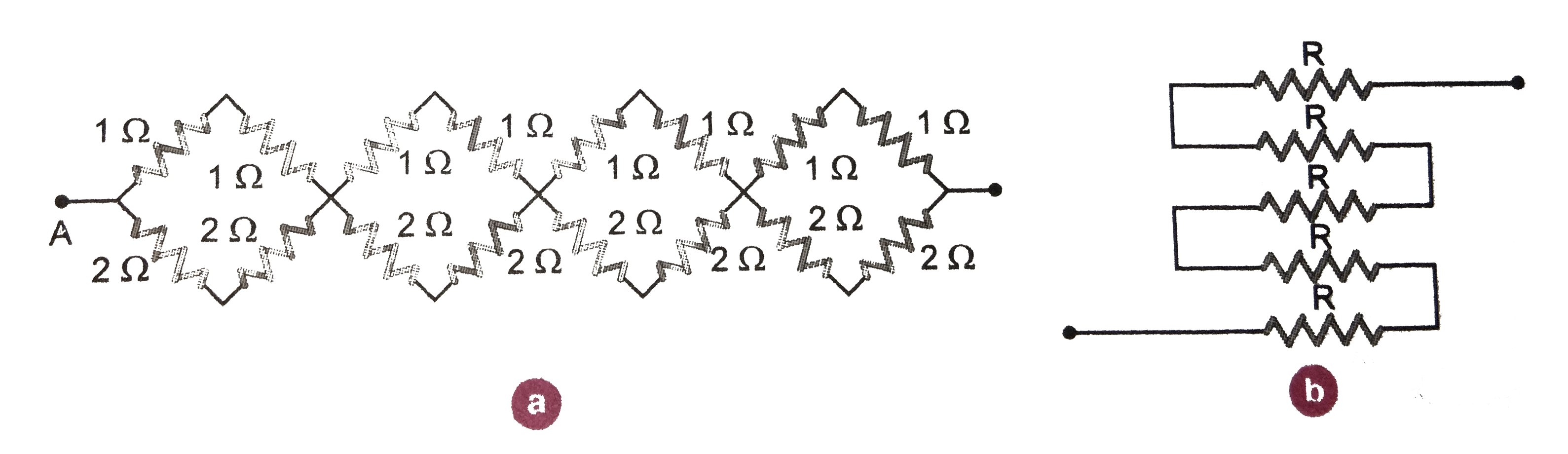(a) Given `n` resistors each of resistance `R`. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of `1 Omega, 2 Omega, 3 Omega`, how will you combine them to get an equivalent resistance of (i) `(11//3)Omega` (ii) `(11//5)Omega` (iii) `6 Omega` (iv) `(6//11) Omega` ?
(c) Determine the equivalent resistance of networks shown in Figure.

Explanation

(a) For maximum effective resistance, the `n` resistors must be connected in series.
Maximum effective resistance, in `R_(s) = nR`.
For minimum effective resistance the `n` resistors must be connected in parallel.
Maximum effective resistance, `R_(p) = R//n :. R_(s)/R_(p) = (nR)/(R//n) = n^(2)`
(b) It is to be noted that (a) the effective resistance of parallel combination of resistors is less than the individual resistance and (b) the effective resistance of series combination of resistors is more than individual resistance.
Case (i) Parallel combination of `1 Omega` and `2 Omega` is connected in series with `3Omega`.
Effective resistance of `1 Omega` and `2 Omega` in parallel will be given by `R_(p)=(1xx2)/(1+2) =2/3Omega`
`:.` Equivalent resistance of `2/3 Omega` and `2 Omega` in series `=2/3+3 = 11/3 Omega`
Case (ii) Parallel combination of `2Omega` and `3Omega` in parallel `=(2xx3)/(2+3)=6/5Omega`
Equivalent resistance of `6/5Omega` and `1Omega` in series `=6/5+1=11/5Omega`
Case (iii) All the resistance are to be connected in series. Now
`:.` Equivalent resistance `(R )` is given by `1/R =1/1+1/2+1/3=(6+3+2)/6=11/6 or R=6/11Omega`
(c) The given net work is a series combination of 4 equal units. Each unit has 4 resistances in which, two resistance (`1Omega` each in series) are in parallel with two other resistances (`2Omega` each in series).
`.:` Effective resistance of two resistance (each of `1Omega`) in series `=1+1 =2Omega`
Effective resistance of two resistances (each of `2Omega`) in series `= 2+2 =4Omega`
If `R_(p)` is the resistance of one unit of resistances, then `1/R_(p) =1/2+1/4 =3/4 or R_(p) =4/3Omega`
`:.` Total resistance of net work (4 such units) `=4/3xx4 =16/4Omega =5.33Omega`
For Figure. `2(NCT).2(b)`,the five resistance each of value `R`, are connected in series.
Their effective resistance `=5R`