Let there be n resistors `R_(1) . . . R_(n)` with `R_(max)=max(R_(1) . . . . R_(n))` and `R_("min")=min{R_(1) . . . R_(n)}`. Show that when they are connected in parallel the resultant resistance `R_(p)=R_("min")` and when they are connected in series, the resultant resistance `R_(S) gt R_(max)`. Interpret the result physically.

Explanation

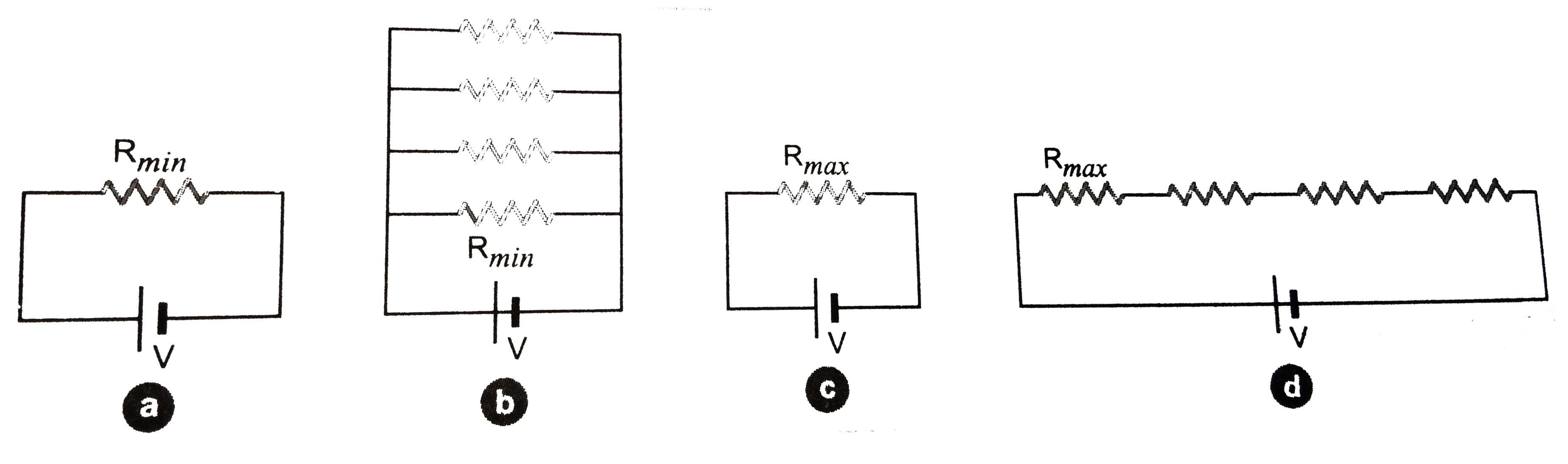
Let `R_(max)` and `R_(min)` be the maximum value and minimum value of the given `n` unequal resistors. When `n` resistors are connected in parallel, the effective resistance `R_(p)` is
`1/R_(p) = 1/R_(1) + 1/R_(2) +…+1/R_(n) :. R_(min)/R_(p) = R_(min)/R_(1) + R_(min)/R_(2) +...+R_(min)/R_(n)`
As `R_(p)` is less than the minimum resistance `R_(min)`, so `R_(min)/R_(p) gt 1` OR `R_(min) gt R_(p) or R_(p) lt R_(min)`
When `n` resistors are in series, then `R_(s) = R_(1)+R_(2) +...+ R_(n)`
As `R_(s)` is greater than the max. resistance `R_(max) :. R_(s) gt R_(max)`
In Fig., due to one resistor of resistance `R_(min)`, there is only one route for the current in circuit. When `n` resistors are in parallel, Fig there are additional `(n-1)` routes for the current in circuit. Therefore `R_(min) gt R_(p) or R_(p) lt R_(min)`.
In Fig. 2(EP).10(c) and (d), due to one resistor of resistance `R_(max)`, the current in circuit is more than the current due to the `n` resistors in series of effective resistance `R_(s)`. So `R_(s) gt R_(max)`.