A resistance is in the shape of a turnacated right circuit cone The radit are a and b `(bgt a)` the special resistance of the material is `p` and the alitude is `h` If laper is small then find the resistance between the plate faces of the resistor

Explanation

Consider an electron of truncested right circuit cone of width `dx` at a distance `x` from and A The resistance of element is

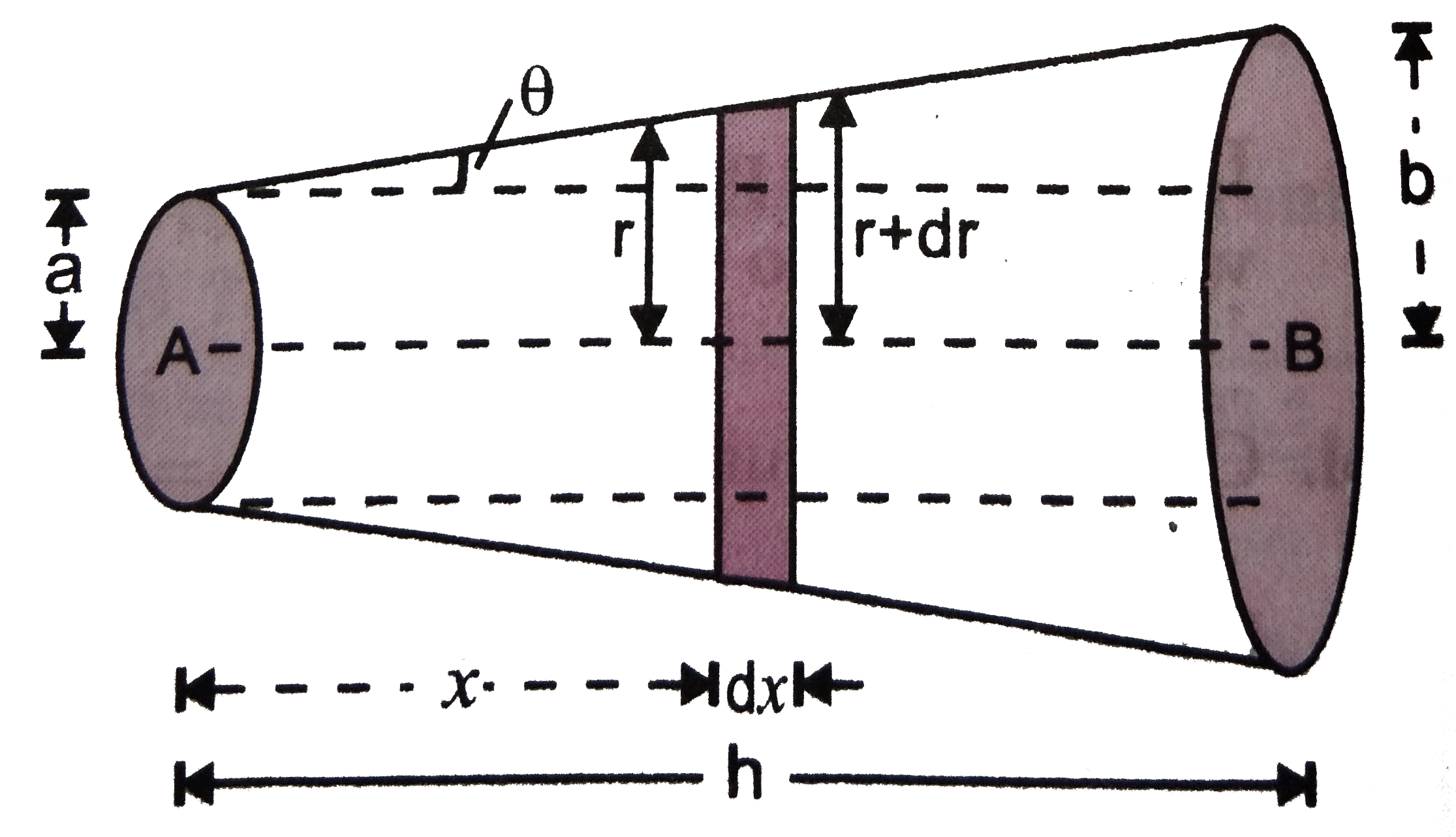
`dR = (pdx)/(pi r^(2))` …(i)
from figure `tan theta = (b - a)/(h) = (dr)/(dx) or dx = (dr)/((h - a)) h`
putting this value in (i) we get
`dR = (p dr h)/(( h - a) pir^(2))= (ph)/(pi(b - a))(dr)/(r^(2))`
The net resistance of conical condition is given by
`R = int_(a)^(b) (ph)/(pi(b - a)) (dr)/(r^(2)) = (ph)/(pi(b - a)) [-(1)/(r )]_(a)^(b)`
`= (ph)/(pi(b - a)) (b-n)/(pi ab)`