Text Solution
Verified by Experts
Topper's Solved these Questions
THERMODYNAMICS AND MOLECULAR PHYSICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Liquids Capillary Effects|25 VideosTHERMODYNAMICS AND MOLECULAR PHYSICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Phase Transformations|35 VideosTHERMODYNAMICS AND MOLECULAR PHYSICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Kinetic Theory Of Gases|51 VideosPHYSICAL FUNDAMENTALS OF MECHANICS
IE IRODOV, LA SENA & SS KROTOV|Exercise Relativistic Mechanics|49 Videos
Similar Questions
Explore conceptually related problems
IE IRODOV, LA SENA & SS KROTOV-THERMODYNAMICS AND MOLECULAR PHYSICS-The Second Law Of Thermodynamics - Entropy
- Find the entropy increment of one mole of a Van der Waals gas due to t...
Text Solution
|
- One mole of a Van der Waals gas which had initially the volume V1 and ...
Text Solution
|
- At very low temperatures the heat capacity of crystals os equal to C =...
Text Solution
|
- Find the entropy increment of an aluminium bar of mass m = 3.0 kg on i...
Text Solution
|
- In some process the temperature of a substance depends on its entropy ...
Text Solution
|
- Find the temperature T as a function of the entropy S of a substance f...
Text Solution
|
- One mole of an ideal gas with heat capacity CV goes through a process ...
Text Solution
|
- A working substance goes through a cycle within which the absolute tem...
Text Solution
|
- One of the two thermally insulated vessels inferconnected by a tube wi...
Text Solution
|
- A weightless piston divides a thermally insulated cylinder into two eq...
Text Solution
|
- An ideal gas was expanded from these initial state to the volume V wit...
Text Solution
|
- A thermally insulated vessel is partitioned into two parts so that the...
Text Solution
|
- A piece of copper of mass m1 = 300 g with initial temperature t1 = 97 ...
Text Solution
|
- Two identical thermally insulated vessels interconnected by a tube wit...
Text Solution
|
- N atoms of gaseous helium are enclosed in a cubic vessel of volume 1.0...
Text Solution
|
- Find the statistical weight of the most probable distribution of N = 1...
Text Solution
|
- A vessel contains N molecules of an ideal gas. Dividing mentally the v...
Text Solution
|
- A vessel of volume V0 contains N molecule of an ideal gas. Find the pr...
Text Solution
|
- An ideal gas in under standard conditions. Find the diameter of the sp...
Text Solution
|
- One mole of an ideak gas consisting of monatomic molecules is enclosed...
Text Solution
|
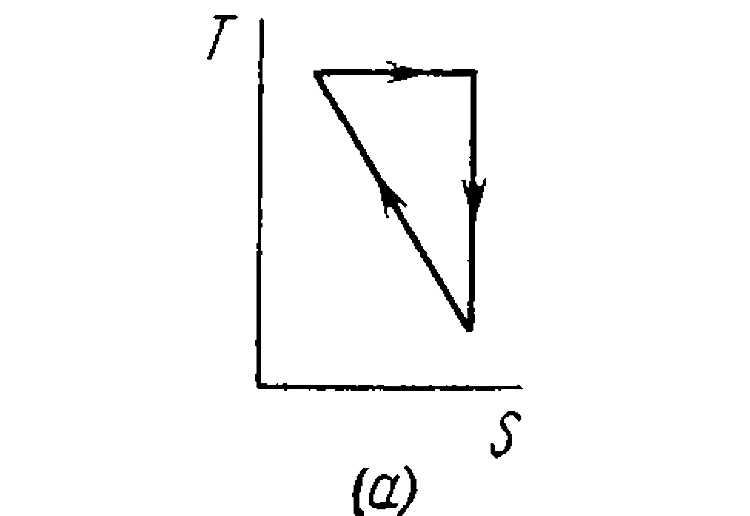
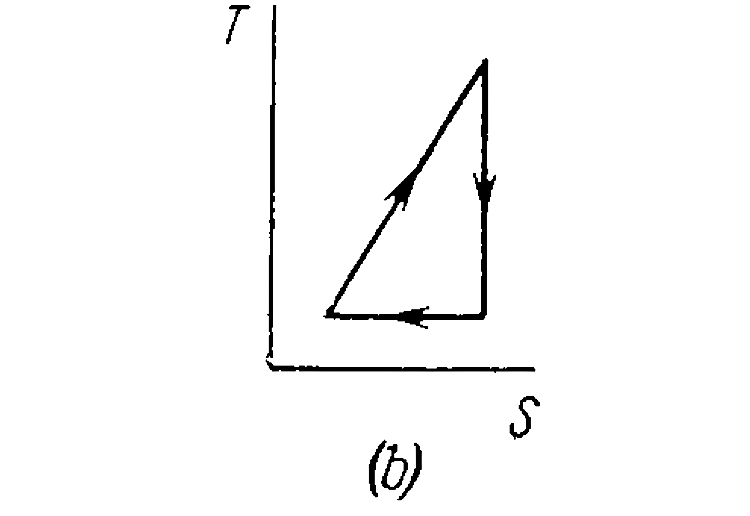 .
. ,
,  .
.