Similar Questions
Explore conceptually related problems
Recommended Questions
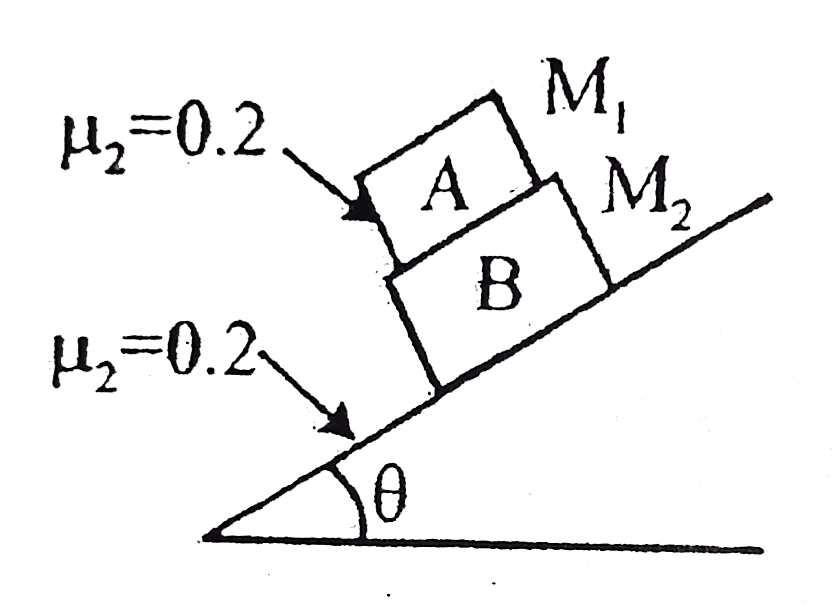
- Two block M(1) and M(2) rest upon each other on an inclined plane Coef...
Text Solution
|
- Two blocks of masses m(1) and m(2) are connected through a massless in...
Text Solution
|
- Two blocks m(1) and m(2) are allowed to move without friction Block m(...
Text Solution
|
- Two blocks m(1) and m(2) are allowed to move without friction Block m(...
Text Solution
|
- Two block M(1) and M(2) rest upon each other on an inclined plane Coef...
Text Solution
|
- Two blocks are kept on an inclined plane and tied to each other with a...
Text Solution
|
- Two blocks of masses m(1) and m(2) kept touching each other on an incl...
Text Solution
|
- Two blocks m(1)=4 kg and m(2)=2 kg connected by a weightless rod on a ...
Text Solution
|
- Two blocks m(1) and m(2) are allowed to move without friction. Block m...
Text Solution
|