लिखित उत्तर
Verified by Experts
NOOTAN HINDI-पृष्ठीय क्षेत्रफल और आयतन -बहुविकल्पीय प्रश्न
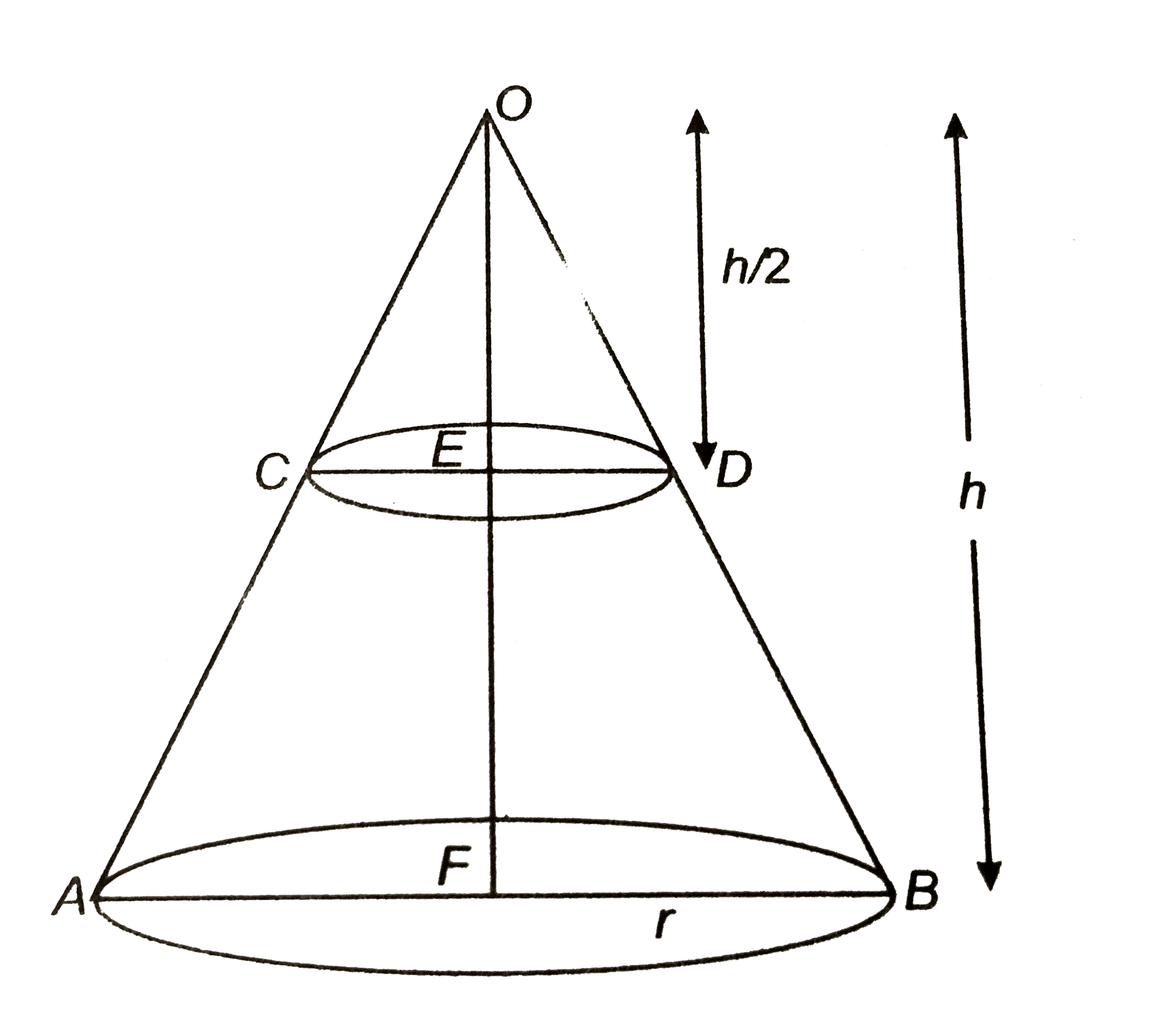
- एक शंकु को इसके अक्ष के मध्य - बिन्दु से आधार के समान्तर समतल द्वारा द...
Text Solution
|
- एक सुराही निम्नलिखित का संयोजन है :
Text Solution
|
- एक गिलास ( आकृति देखिए ) का आकार प्रायः निम्न होता है :
Text Solution
|
- एक साहुल ( आकृति देखिए ) निम्नलिखित का संयोजन है :
Text Solution
|
- विमाओं 49 सेमी xx33 सेमी xx24 सेमी के घनाभ का आकार के लोहे के किसी ठोस...
Text Solution
|
- ठोस को एक आकार से दूसरे में बदलने पर, नए आकार का आयतन :
Text Solution
|
- दो गोलों के पृष्ठों का अनुपात 16:9 है । इनके आयतनों का अनुपात है :
Text Solution
|
- त्रिज्या r सेमी और ऊंचाई h सेमी (hgt 2r) वाले एक लम्बवृत्तीय बेलन मे...
Text Solution
|