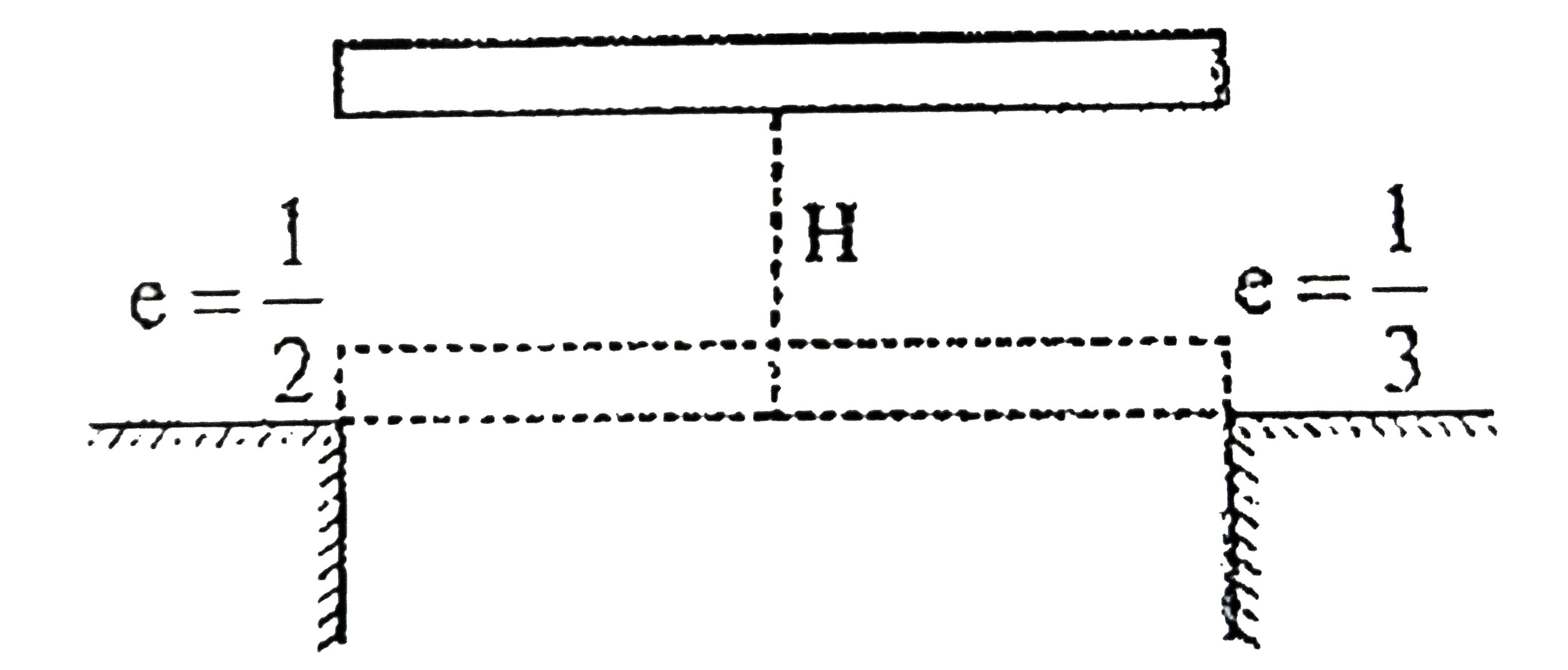
A uniform horizontal rod of length l is dropped from height H above th two fixed edge shown in the diagram. If coefficient of restitution between the rod and fixed edges are `(1)/(2)` and `(1)/(3)` then find direction of angular velocity of the rod about it's centre of mass after the impact.

A uniform horizontal rod of length l falls vertically from height h on two identical blocks placed symmertrically below the rod as shown in figure the coefficients of restitution are e _(1) and e_(2) the maximum height through which the centre of mass of the rod will rise after after bouncing off the blocks is

A uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.

A particle of mass m=1 kg collides with the end with velocity v_(0)=6 ms^(-1) of a spinning rod of mass 2m and length l=1 m at the end of the rod. If the coefficient of restitution of collision e=(2//3), find the a. velocity of the particle b. angular velocity of the rod just after the impact.

A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a/4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.

A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a/4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.

A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a/4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.

A uniform rod of length L lies on a smooth horizontal table. The rod has a mass M . A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision. Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.

A uniform rod of length lambda lies on a smooth horizontal table A particle moving on the table has a mass m and a speed v before the collision and it sticks to the rod after the collision. The rod has a mass M then find out. The velocity of the centre of mass C and the angular velocity of the system about the centre of mass after the collision.

A rod of length l forming an angle theta with the horizontal strikes a frictionless floor at A with its centre of mass velocity v_(0) and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.

A rod of length l forming an angle theta with the horizontal strikes a frictionless floor at A with its centre of mass velocity v_(0) and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.