लिखित उत्तर
Verified by Experts
टॉपर्स ने हल किए ये सवाल
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
NOOTAN HINDI|Exercise अतिलघु उत्तरीय प्रश्न|10 Videosसमान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
NOOTAN HINDI|Exercise लघु उत्तरीय प्रश्न|10 Videosसमान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
NOOTAN HINDI|Exercise प्रश्नावली 9.3|16 Videosचतुर्भुज
NOOTAN HINDI|Exercise विविध प्रश्नावली|24 Videos
NOOTAN HINDI- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल -प्रश्नावली 9.4
- समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत...
Text Solution
|
- आकृति में, भुजा BC पर दो बिन्दु D और E इस प्रकार स्थित है कि BD = DE =...
Text Solution
|
- आकृति में ABCD, DCFE और ABFE समान्तर चतुर्भुज है। दर्शाइए कि ar(ADE) =...
Text Solution
|
- आकृति में, ABCD एक समान्तर चतुर्भुज है और BC को एक बिन्दु Q तक इस प्रक...
Text Solution
|
- आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार है कि D भुजा BC का म...
Text Solution
|
- चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु P पर प्रतिच्छेद करते है...
Text Solution
|
- P और Q क्रमशः त्रिभुज ABC की भुजाओं AB और BC के मध्य-बिन्दु है तथा R र...
Text Solution
|
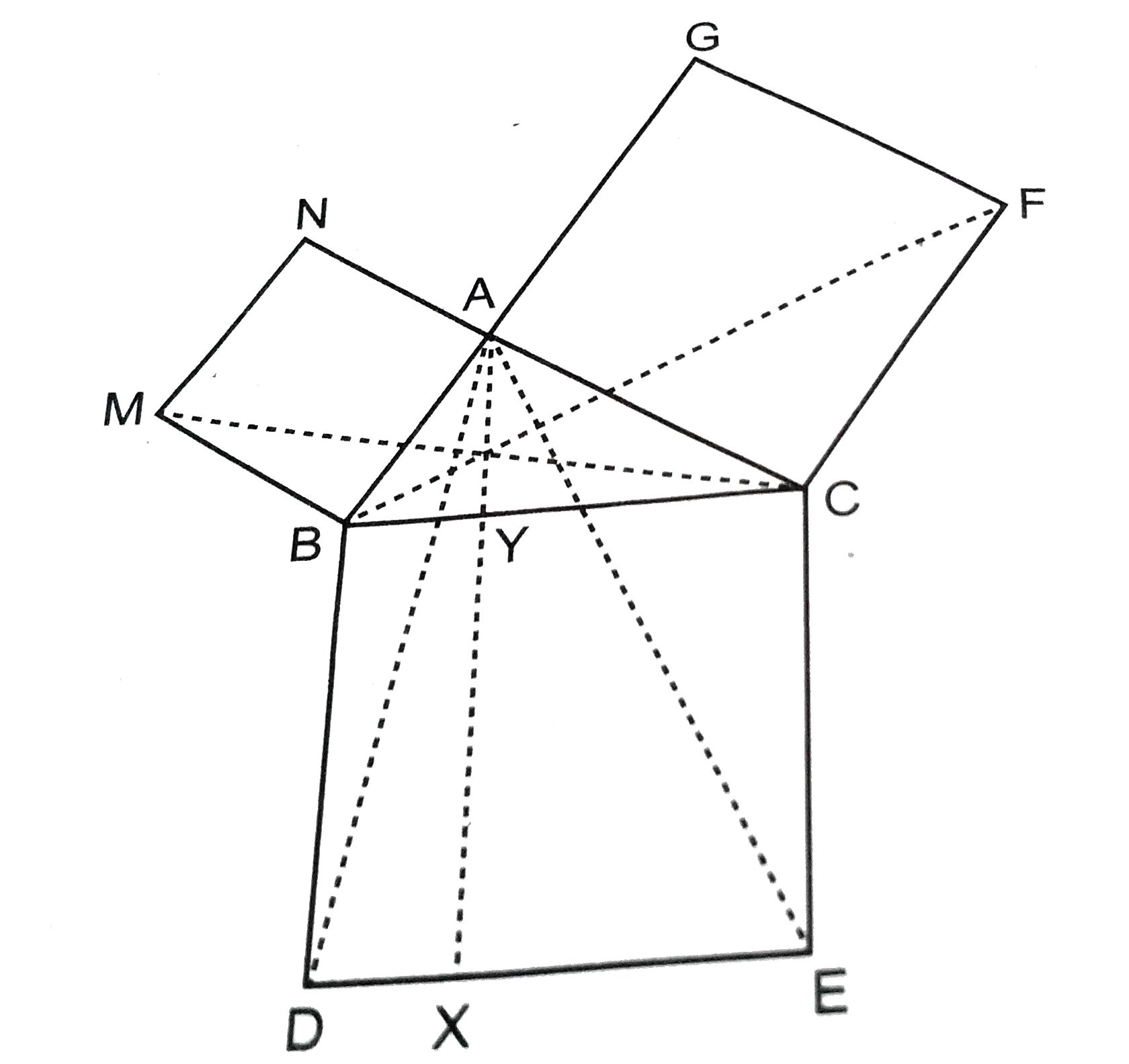
- आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और...
Text Solution
|