A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MARVEL PUBLICATION-REFRACTION OF LIGHT -Test Your Grasp
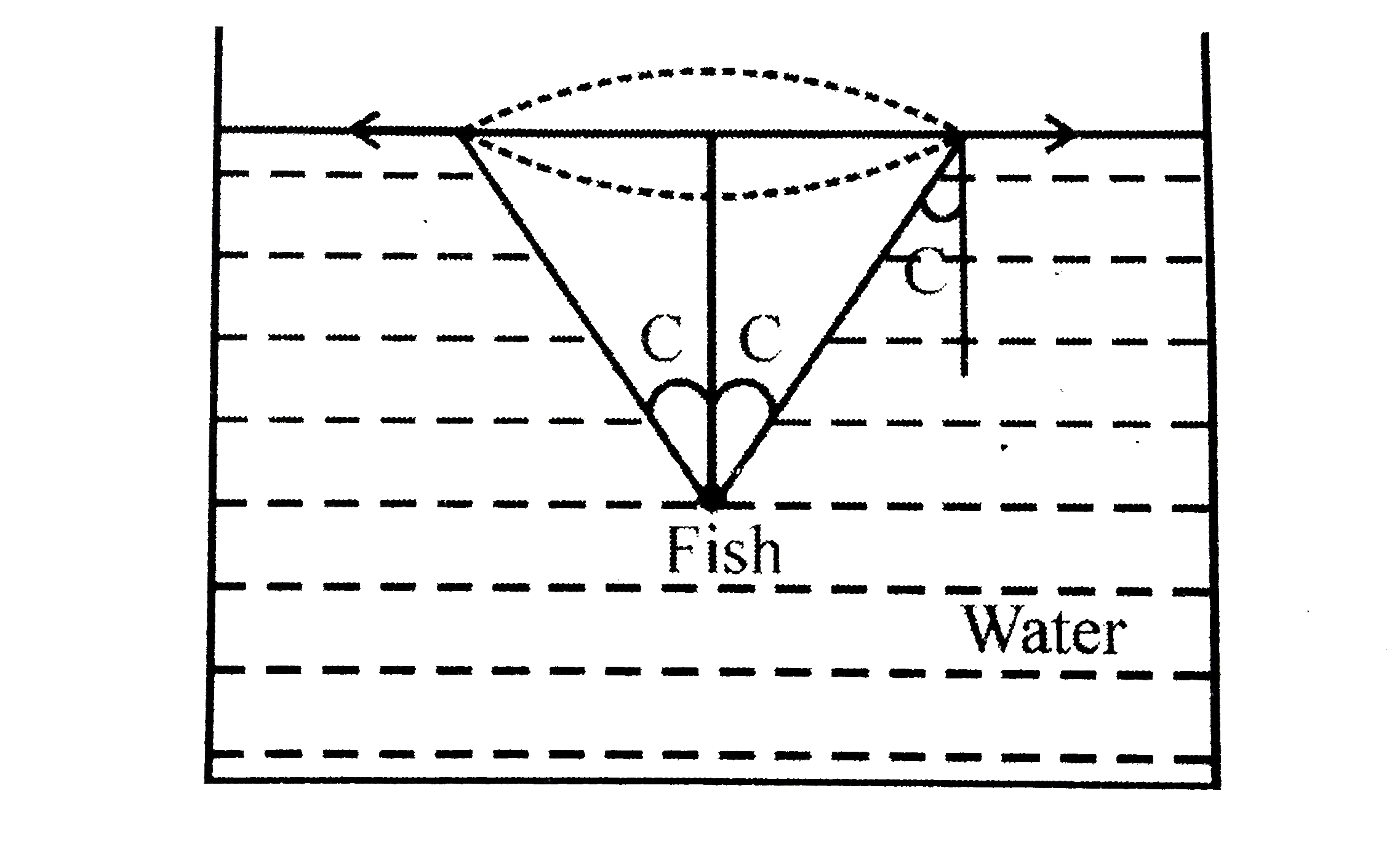
- When the surface of a lake is calm , a fish submerged in water will se...
Text Solution
|
- The refractive index of glass w.t.r. a medium is 4/3 . If vm - vg = 6....
Text Solution
|
- A ray of light traveling in a tranparent medium falls on a surface sep...
Text Solution
|
- Light takes t(1) second to travel a distance x cm in vacuum and the sa...
Text Solution
|
- A ray of light suffers minimum deviation while passing through a prism...
Text Solution
|
- A ray of light passing through a prism having refractive index sqrt2 s...
Text Solution
|
- The angle of incidence for a ray of light at a refracting surface of a...
Text Solution
|
- An air bubble in a glass slab with refractive index 1.5 (near normal i...
Text Solution
|
- A thin prism having refracting angle 10^(@) is made of glass of refrac...
Text Solution
|
- If the scattering intensity of a liquid is 8 units at a wavelentth of ...
Text Solution
|
- A bulb is placed at a depth of 2sqrt7cm in water and a floating opaque...
Text Solution
|