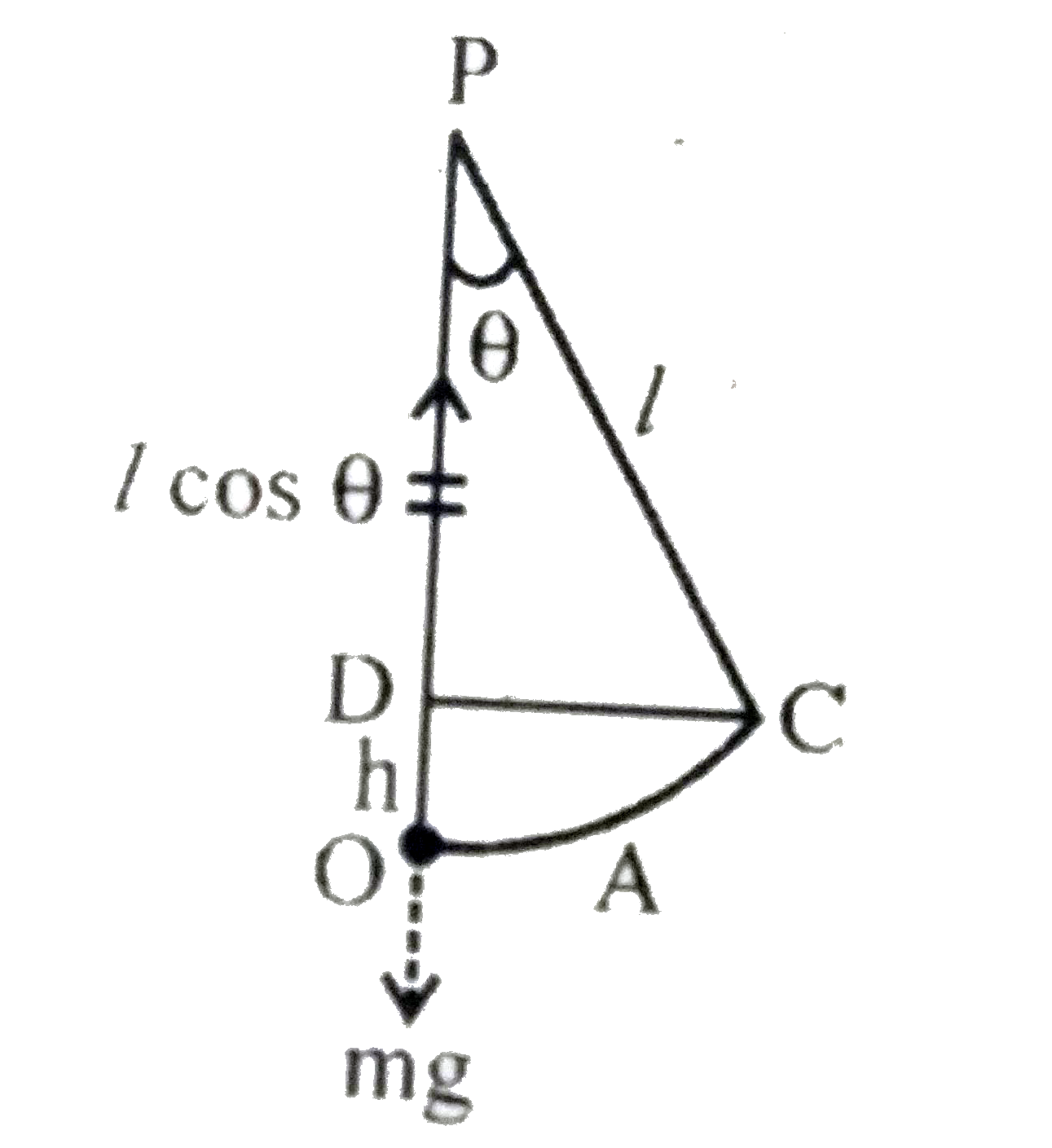
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MARVEL PUBLICATION-OSCILLATIONS-MCQ
- The length of a second's pendulum on the surface of earth is 1 m. What...
Text Solution
|
- A simple pendulum has a time period T(1) when on the earth's surface a...
Text Solution
|
- A simple pendulm has a length L and a bob of mass M. The bob is vibrat...
Text Solution
|
- The equation (d^2y)/(dt^2)+b(dy)/(dt)+omega^2y=0 represents the eq...
Text Solution
|
- The amplitude of a vibrating body situated in a resisting medium
Text Solution
|
- In case of a forced vibration, the resonance wave becomes very sharp w...
Text Solution
|
- Four pendulums A,B,C and D are suspended from the same elastic support...
Text Solution
|
- When a dampled harmonic oscillator completes 100 oscillations, its amp...
Text Solution
|
- A body of mass 0.25 kg is attached to a vertical spring. The spring is...
Text Solution
|
- Amplitude of a wave is represented by A(c)/(a+b+c) Then resonance will...
Text Solution
|
- The amplitude of damped oscillator becomes half in one minute. The amp...
Text Solution
|
- When a tuning fork of frequency 262 Hz is struck, it loses half of its...
Text Solution
|
- A block off mass 200 g executing SHM under the unfluence of a spring o...
Text Solution
|
- A block of mass one kg is fastened to a spring with a spring constant ...
Text Solution
|
- A particle which is attached to a spring oscillates in a horizontal pl...
Text Solution
|
- Two spring are connected toa block of mass M placed a frictionless sur...
Text Solution
|
- A rubber band (two parallel strands of elastic material) has a force c...
Text Solution
|
- A body of mass of 4 kg is mounted on four vertical springs each having...
Text Solution
|
- Three mass 0.1 kg ,0.3 kg and 0.4 kg are suspended at end of a spring....
Text Solution
|
- Two springs fixed at one end are stretched by 4 cm and 12 cm, respecti...
Text Solution
|