Similar Questions
Explore conceptually related problems
Recommended Questions
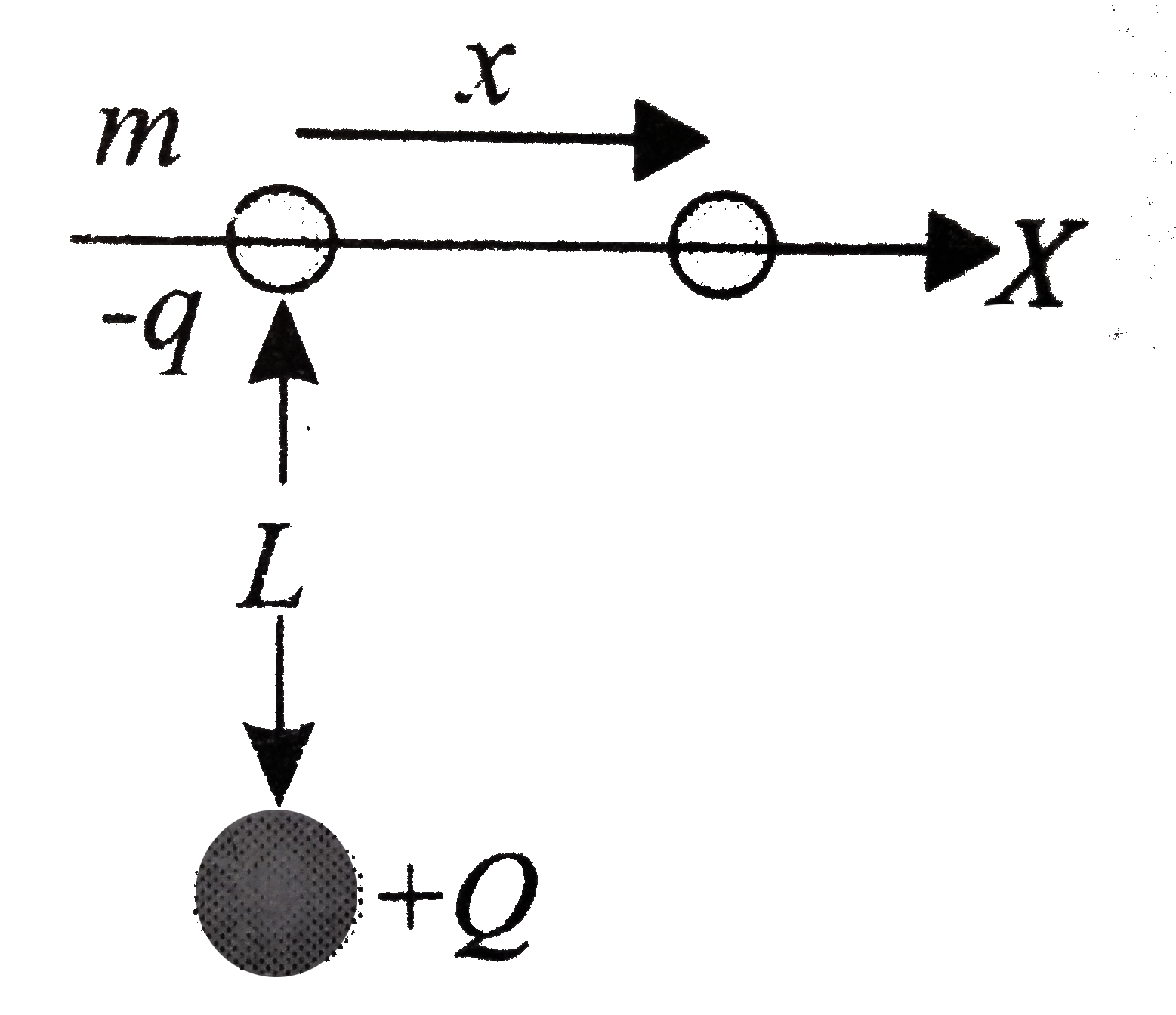
- A small beads of mass ma having charge -q is constrained to move along...
Text Solution
|
- A charge particle q is released at a distance R(@) from the infinite l...
Text Solution
|
- Two identical beads each have a mass m and charge q. When placed in a ...
Text Solution
|
- A thin insulating wire is stretched along the diameter of an insulated...
Text Solution
|
- A small point mass m has a charge q, which is constrained to move insi...
Text Solution
|
- Two small beads having positive charges 3q and q are fixed at the oppo...
Text Solution
|
- A small beads of mass ma having charge -q is constrained to move along...
Text Solution
|
- Two identical charges +Q are kept fixed some distance apart.A small pa...
Text Solution
|
- Two identical positive charges Q each are placed on the x axis at poin...
Text Solution
|