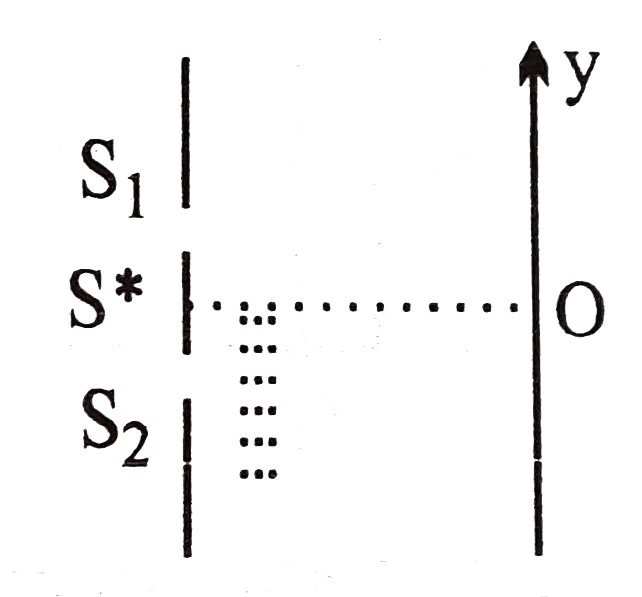Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The young's double slit experiment is done in a medium of refractive i...
Text Solution
|
- A YDSE is performed in a medium of refractive index 4 // 3, A light of...
Text Solution
|
- A YDSE is performed in a medium of refractive index 4 // 3 , A light o...
Text Solution
|
- A YDSE is performed in a medium of refractive index 4 // 3 , A light o...
Text Solution
|
- The young's double slit experiment is done in a medium of refractive i...
Text Solution
|
- The young's slit experiment is done in a medium of refractive index 4/...
Text Solution
|
- Young’s double slit experiment is done in a medium of refractive index...
Text Solution
|
- In Young's double slit experiment the point source is placed slightly ...
Text Solution
|
- The young's double slit experiment is done in a medium of refractive i...
Text Solution
|