Home
Class 12
PHYSICS
In a YDSE two him transparent sheet are ...

In a YDSE two him transparent sheet are used in front of the slits `S_(1)`&`S_(2)` having `mu_(1)=1.6`and `mu_(2)=1.4` respectively.If both sheets have thickness`t` ,the central maximum is observed at a distance of `5mm`from center`O`.Now the sheets are replaced by another two sheets each of refractive index `(mu_(1)-mu_(2))/(2)` but having thickness `t_(1)&t_(2)=(t_(1)-t_(2))/(2)`.Now central maximum is observed at distance of `8mm` from center`O` on the same side as before.Find the thickness `t_(1)` (in`mu`m) [Given:d=1mm,D=1m]

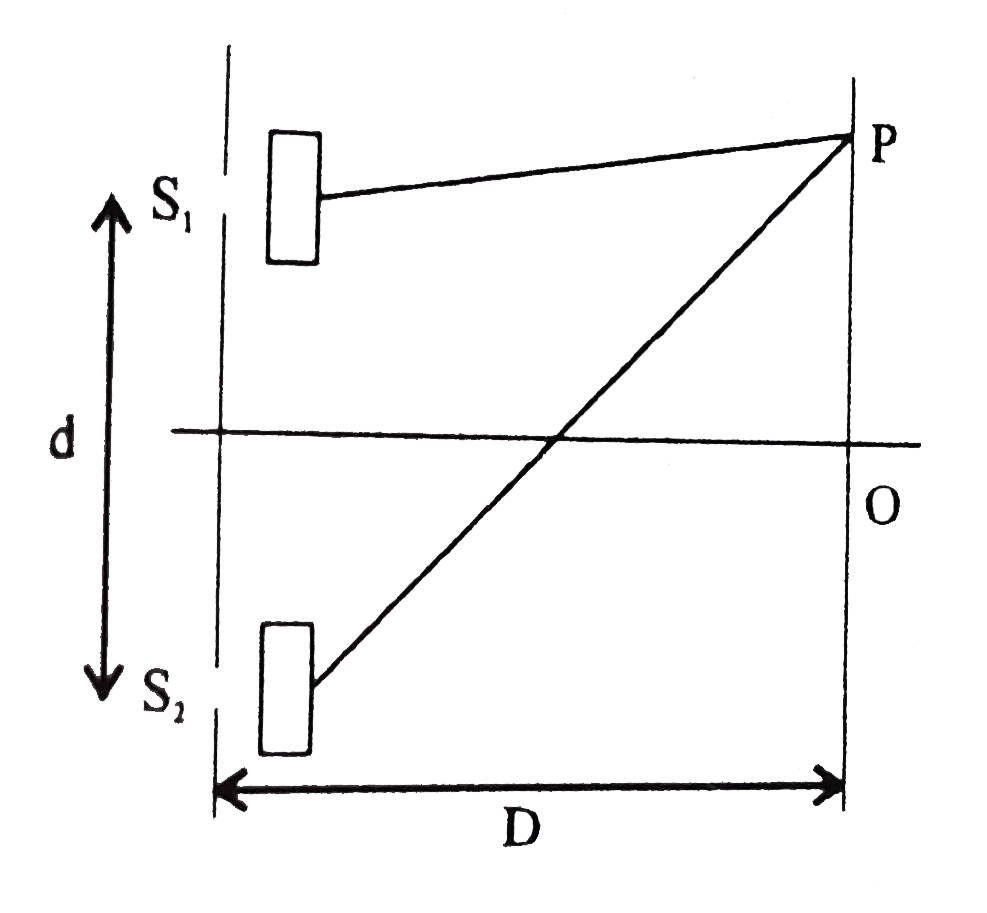
Text Solution

Verified by Experts

The correct Answer is:
`33`
Path difference =`(S_(2)P-t+mu_(2)t)-(S_(1)P-t+mu_(1)t)`
`=(S_(2)P-S_(1)P)+(mu_(2)-mu_(1))t`
`=(x_(1)d)/(D)+(mu_(2)-mu_(1))t….(1)`
For central maximum at `P`, path difference=`0`
`(x_(1)d)/(mu_(2)-mu_(1))t=0 rArr (x_(1)d)/(D)=(mu_(1)-mu_(2))t`
`5(d)/(D)=(1.6-1.4)t rArr 0.2t=(5xx10^(-3)xx1xx10^(-3))/(1)`
`t=25mu m`
since `(mu_(1)+mu_(2))/(2)=1.5`
Now path difference =`{S_(2)P-t_(2)+(mu_(1)+mu_(2))/(2)t_(2)}-{S_(1)P-T_(1)+(mu_(1)+mu_(2))/(2)t_(1)}`
`=S_(2)P-S_(1)P+(t_(1)-t_(2))+(mu_(1)-mu_(2))/(2) (t_(2)-t_(1))`
`=(x_2d)/D+(t_1-t_2)+(mu_1+mu_2)/2(t_2-t_1)`
For central maximum path difference=`0`
`(x_(2)d)/(5)+(t_(1)-t_(2))+(mu_(1)+mu_(2))/(2)(t_(2)-t_(1))=0 rArr (x_(2)d)/(5)=t_(1)-t_(2)((mu_(1)+mu_(2))/(2)-1)`
`(8xx10^(-3)xx11xx10^(-3))/(1) =(t_(1)-t_(2))(1.5-1)`
`t_(1)-t_(2)=16xx10^(-6)`
`t_(1)-t_(2)=16mum...(2)`
Given that `(t_(1)+t_(2))/(2)=t rArr t_(1)+t_(2)=2t`
`t_(1)+t_(2)=50mum...(3)`
from(2)&(3)
`2t_(1)=66mum`
`t_(1)=33mum`
Promotional Banner

Similar Questions

Explore conceptually related problems

If a ray of light takes t_(1) and t_(2) times in two media of absolute refractive indices mu_(1) and mu_(2) respectively to travel same distance, then

Two slits S_(1) and S_(2) illuminated by a white light source give a white central maxima. A transparent sheet of refractive index 1.25 and thickness t_(1) is placed in front of S_(1) . Another transparent sheet of refractive index 1.50 and thickness t_(2) is placed in front of S_(2) . If central maxima is not effected, then ratio of the thickness of the two sheets will be :

To make the central fringe at the center O , mica sheet of refractive index 1.5 is introduced Choose the corect statement(S).

In the YDSE shown below, two slits are covered with thin sheets having a thickness t and 2t and refractive indices 2mu and mu respectively. The position of central maxima is shifted by a distance of N (in cm) from the central position of the screen. Find the value of N. [d=1 mm, D = 1 m, t = 2xx10^(-2)mm,mu=(3)/(2)]

In YDSE, let A and B be two slits. Films of thickness t_(A) and t_(B) and refractive mu_(A) and mu_(B) are placed in front of A and B, respectively. If mu_(A) t_(A) = mu_(A) t_(B) , then the central maxima will

A stationary swimmer S , inside a liquid of refractive index mu_(1) , is at a distance d from a fixed point P inside the liquid. A rectangular block of width t and refractive index mu_(2)(mu_(2) lt mu_(1)) is now placed between S and P.S will observer P to be at a distance

In YSDE, both slits are covered by transparent slab. Upper slit is covered by slab of R.I. 1.5 and thickness t and lower is covered by R.I. 4/ 3 and thickness 2t, then central maxima

Two transparent sheets of thickness t_(1) and t_(2) and refractive indexes mu_(1) and mu_(2) are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O? [(D[(mu_(1)-1)t_(1)-(mu_(2)-1)t_(2)])/(d),(mu_(2)-1)t_(2)]

In the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2mu and mu .Find the position (y) of central maxima.