Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
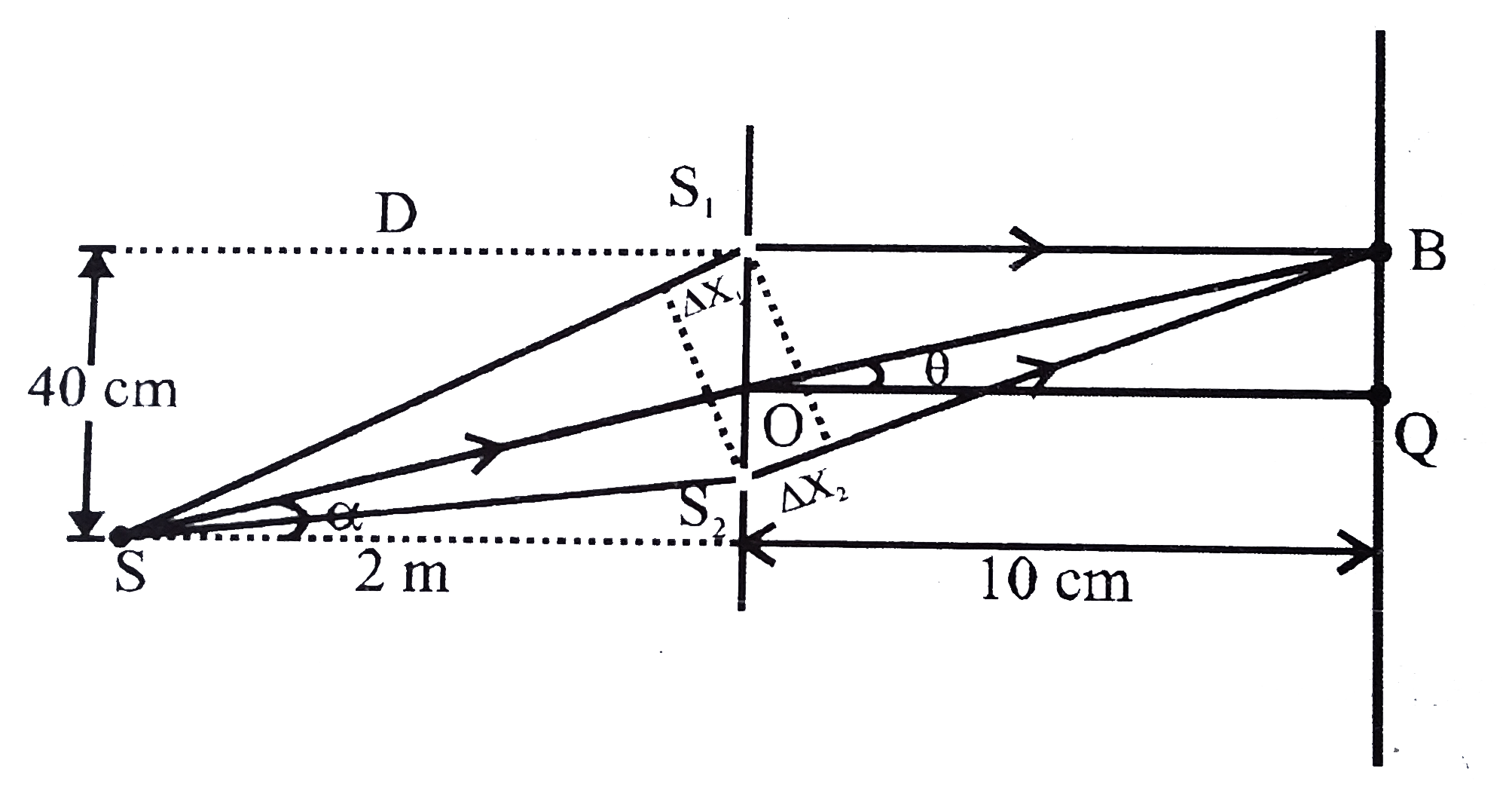
- A vessel ABCD of 10 cm width has two small slits S(1) and S(2) sealed ...
Text Solution
|
- Let S(1) and S(2) be the two slits in Young's double-slit experiment. ...
Text Solution
|
- In a midified YDESE, sources S is kept in front of slit S(1) . Find th...
Text Solution
|
- A vessel ABCD of 10 cm width has two small slits S(1) and S(2) sealed ...
Text Solution
|
- In arrangement shown in figure, plane wavefront of monochromatic light...
Text Solution
|
- 10 cm चौड़ाई वाले एक पात्र ABCD में दो छोटी रेखाछिछ्र (द्वि-स्लिट) S(1...
Text Solution
|
- Two coherent point sources S(1) and S(2) vibrating in phase emit light...
Text Solution
|
- A vessel ABCD of 10 cm width has two small slits s1 and S2 sealed, wit...
Text Solution
|
- A vessel ABCD of 10 cm width has two small slits S(1) and S(2) sealed ...
Text Solution
|