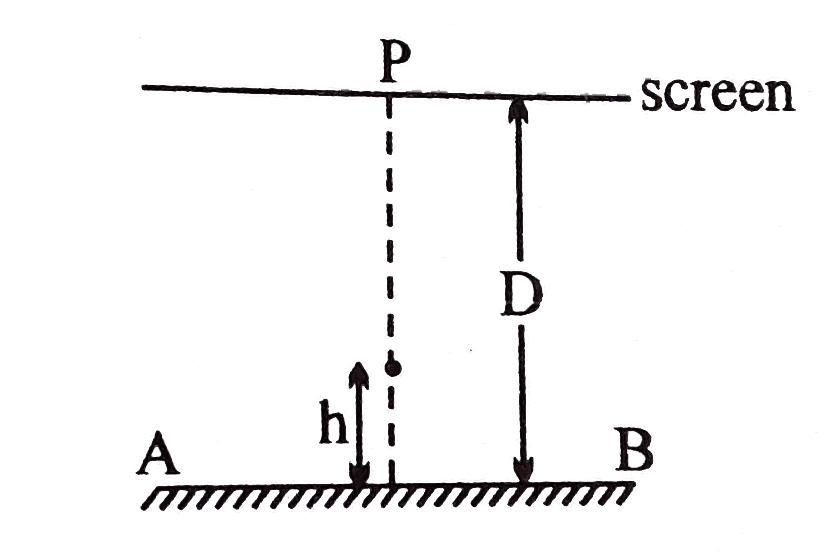Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
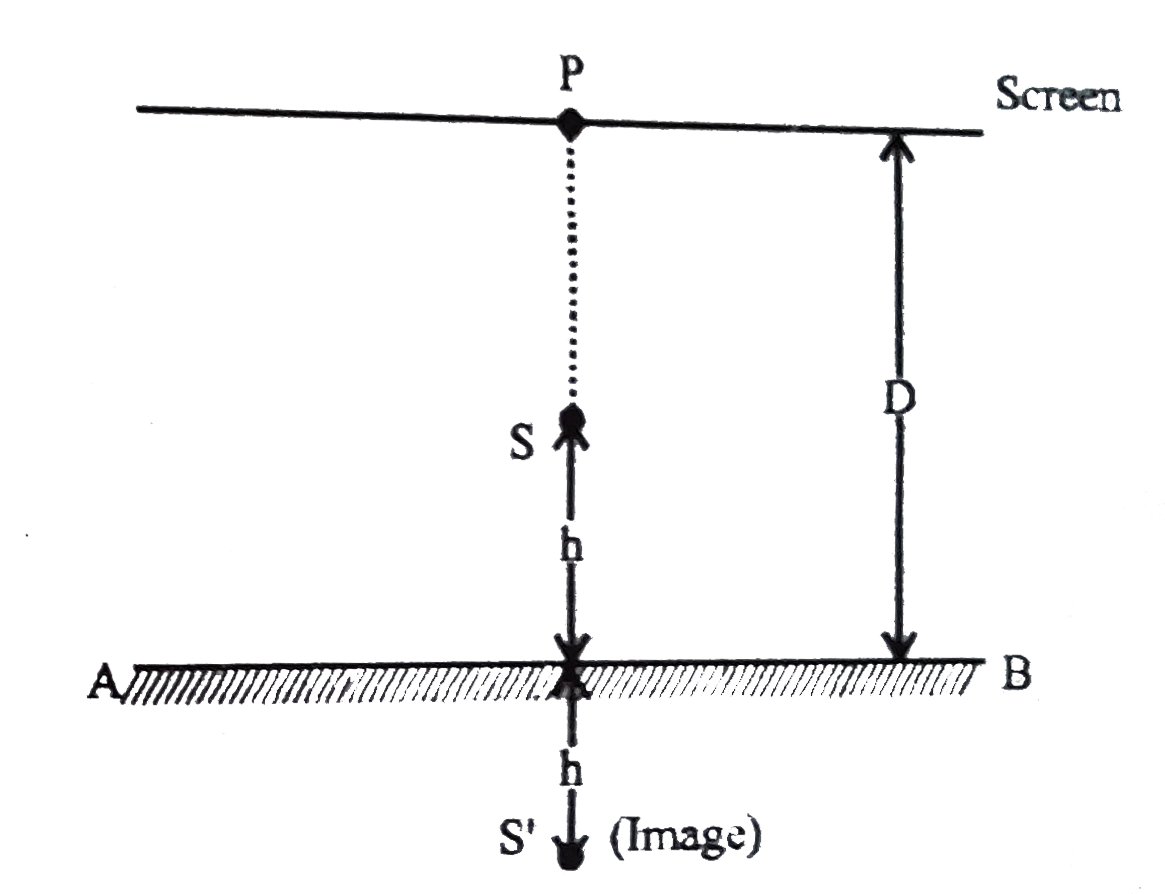
- A point sources S emitting light of wavelength 600nm is placed at a ve...
Text Solution
|
- A point sources S emitting light of wavelength 600nm is placed at a ve...
Text Solution
|
- A point sources S emitting light of wavelength 600nm is placed at a ve...
Text Solution
|
- A point is emitting light of wavelength 6000Å is placed at a very smal...
Text Solution
|
- A point source S emits light of wavelength 600 nm. It is palced at a v...
Text Solution
|
- A point source S emits light of wavelength 600 nm. It is palced at a v...
Text Solution
|
- A point source S emits light of wavelength 600 nm. It is palced at a v...
Text Solution
|
- 600 नैनोमीटर तरंगदैर्ध्य के प्रकाश का उत्सर्जन करने वाला एक बिंदु स्रो...
Text Solution
|
- एक बिन्दु स्त्रोत Sजो 600nm तरंगदैर्ध्य का प्रकाश उत्सर्जित कर रहा है....
Text Solution
|