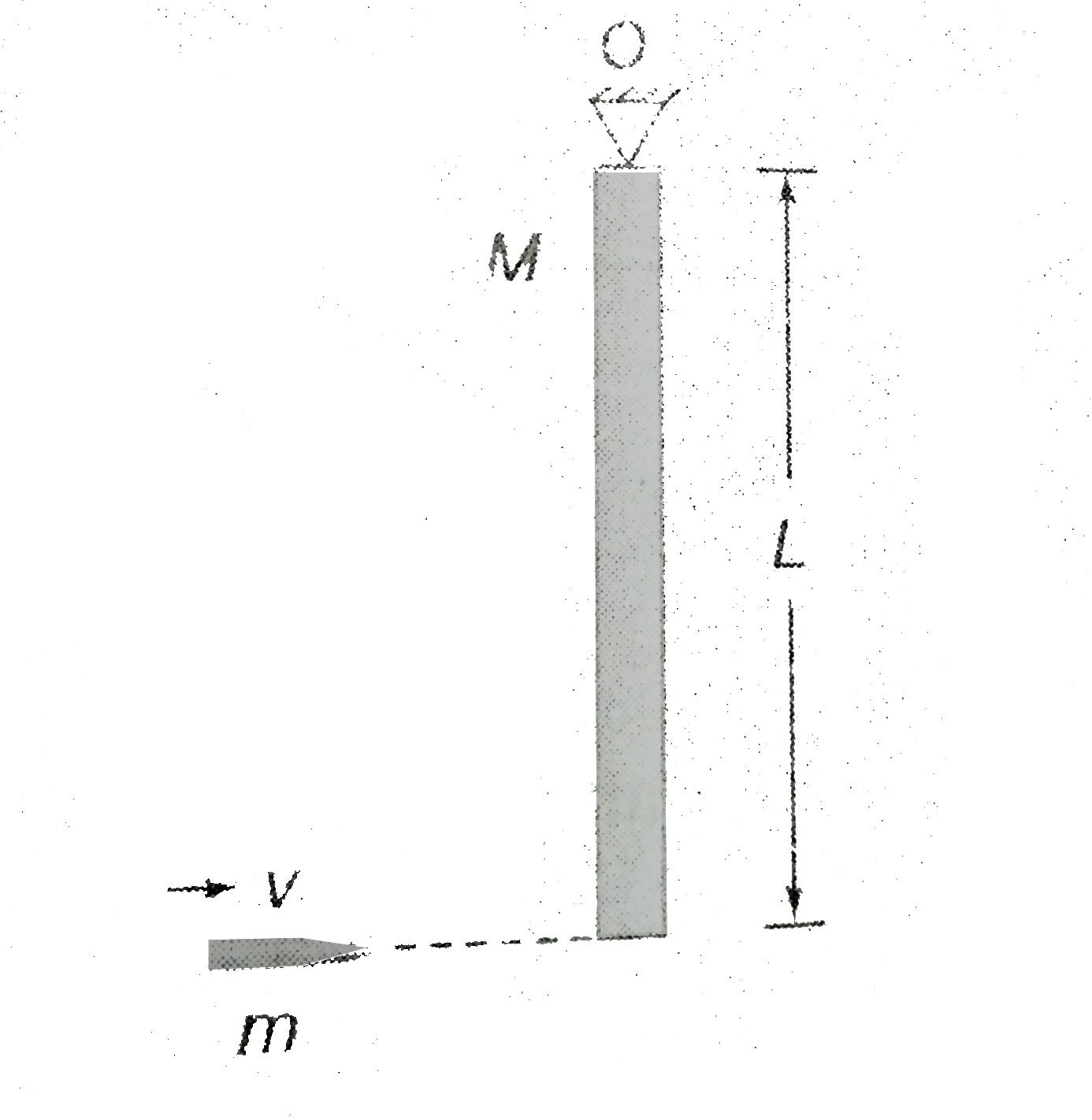Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-ROTATIONAL MOTION-Exercise
- A wooden log of mass M and length L is hinged by a frictionless nail a...
Text Solution
|
- Three point masses, each of mass m, are placed at the corners of an eq...
Text Solution
|
- The moment of inertia of a disc of mass M and radius R about an axis. ...
Text Solution
|
- Let I(A) and I(B) be moments of inertia of a body about two axes A and...
Text Solution
|
- A closed cylindrica tube containing some water (not filling the entire...
Text Solution
|
- A uniform cylinder has radius R and length L. If the moment of inertia...
Text Solution
|
- A solid sphere of mass M, radius R and having moment of inertia about ...
Text Solution
|
- Two circular discs are of same thickness. The diameter of A is twice t...
Text Solution
|
- The moment of inertia of a circular disc of mass M and radius R about ...
Text Solution
|
- From a uniform wire, two circular loops are made (i) P of radius r and...
Text Solution
|
- The moment of inertia of a uniform rod about a perpendicular axis pass...
Text Solution
|
- The density of a rod AB increases linearly from A to B its midpoint is...
Text Solution
|
- The M.I. of a rod about an axis through its center and perpendicular t...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- Three rings, each of mass m and radius r, are so placed that they touc...
Text Solution
|
- Two rings A (2m,R) and B (m,R) are placed such that these are perpendi...
Text Solution
|
- If I(0) is the moment of inertia body about an axis passing through it...
Text Solution
|
- A rod of length L is made of a uniform length L//2 of mass M(1) and a ...
Text Solution
|
- Four spheres each of mass M and diameter 2r, are placed with their cen...
Text Solution
|
- The ratio of the radii of gyration of a circular disc about a tangenti...
Text Solution
|
- One quarter sector is cut from a uniform circular disc of radius R. Th...
Text Solution
|