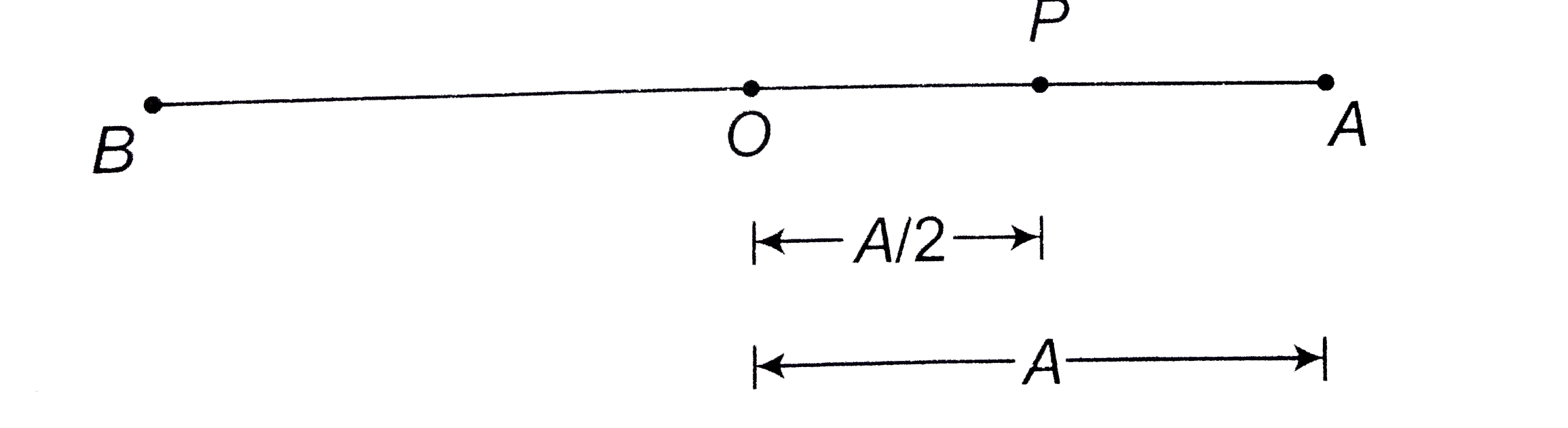Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-SIMPLE HARMONIC MOTION-Exercises
- Consider a simple harmonic motion of time period T. Calculate the time...
Text Solution
|
- Select the correct statements. (i) A simple harmonic motion is neces...
Text Solution
|
- A student says that he had applied a force F=-ksqrtx on a particle and...
Text Solution
|
- Which of the following quantities are always negative in a simple har...
Text Solution
|
- Which of the followign quantities are always zero in a simple harmonic...
Text Solution
|
- The time period of a particle in simple harmonic motion is equal to th...
Text Solution
|
- The average acceleration in one tiome period in a simple harmonic moti...
Text Solution
|
- A partilce is executive simple harmonic motion given by x=5sin(4t-pi...
Text Solution
|
- A particle starts SHM from the mean position. Its amplitude is A and t...
Text Solution
|
- A body of mass 5g is executing SHM with amplitude 10cm, its velocity i...
Text Solution
|
- A particle is vibrating in SHM. If its velocities are v1 and v2 when t...
Text Solution
|
- The phase (at a time t) of a particle in simple harmonic motion tells
Text Solution
|
- Which of the following equation does not represent a simple harmonic m...
Text Solution
|
- Which of the following is a simple harmonic motion
Text Solution
|
- The equation of SHM of a particle is (d^2y)/(dt^2)+ky=0, where k is a ...
Text Solution
|
- A particle is executing SHM. Then the graph of acceleration as a funct...
Text Solution
|
- A particle is executing SHM. Then the graph of velocity as a function ...
Text Solution
|
- For a simple pendulum the graph between length and time period will be
Text Solution
|
- Out of the following function reporesenting motion of a particle which...
Text Solution
|
- A particle excuting S.H.M. of amplitude 4 cm and T = 4 sec .The time t...
Text Solution
|
- A particle is executing SHM of amplitude 4cm and time period 12s. The ...
Text Solution
|