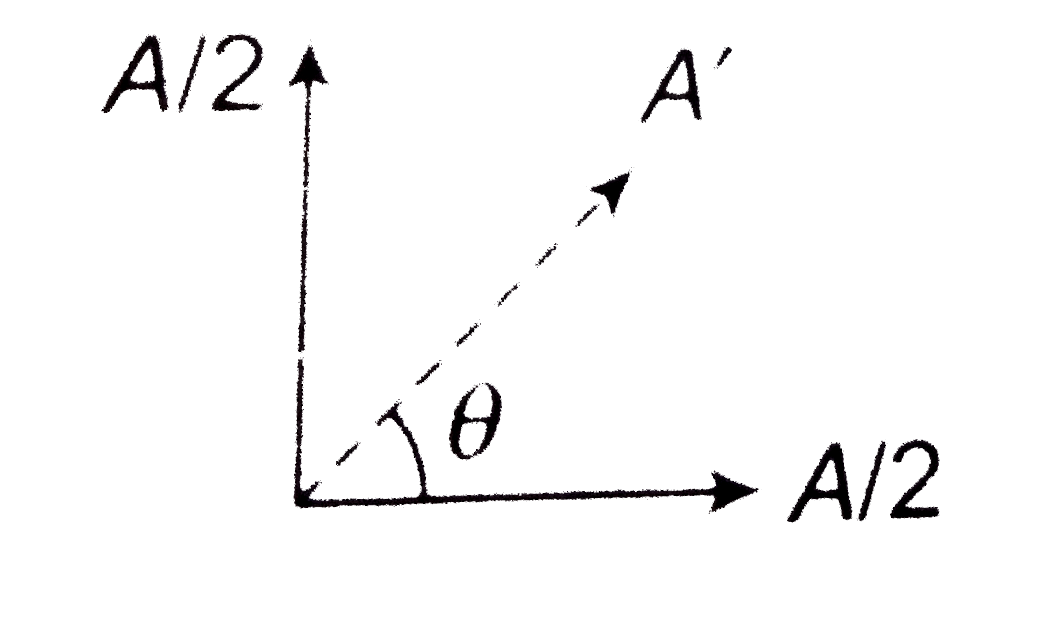A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-SIMPLE HARMONIC MOTION-Exercises
- The motion of a particle is given by x=A sin omegat+Bcos omegat. The m...
Text Solution
|
- A particle moves on the X-axis according to the equation x=A+Bsinomega...
Text Solution
|
- The ratio of the amplitudes of the simple harmonic oscillations given ...
Text Solution
|
- The minimum phase difference between the two simple harmonic oscillati...
Text Solution
|
- A body executes SHM of period 3s under the influence of one force, and...
Text Solution
|
- The displacement of a particle is given by r=A(haticosomegat+hatjsinom...
Text Solution
|
- Electrons in an oscilloscope are deflected by two mutually perpendicul...
Text Solution
|
- Two particles A and B execute simple harmonic motions of period T and ...
Text Solution
|
- Two simple pendulum of length 5m and 20m respectively are given small ...
Text Solution
|
- Two simple pandulum whose lengths are 100cm and 121cm are suspended si...
Text Solution
|
- Two particles execute SHM of the same time period along the same strai...
Text Solution
|
- Two pendulum of lengths 1m and 16m are in phase at the mean position a...
Text Solution
|
- Time period of is simple pendulum of length L is T(1) and the point ti...
Text Solution
|
- A disc of radius R and mass M is plvoted at the rim and is set for sma...
Text Solution
|
- The composition of two simple harmonic motions of equal periods at rig...
Text Solution
|
- The amplitude and maximum velocity will be respectively X= 3 sin 2t +...
Text Solution
|
- A particle moves on the X-axis according to the equation x=x0 sin^2ome...
Text Solution
|
- A particle moves in the X-Y plane according to the equation vecr=(veci...
Text Solution
|
- A point mass is subjected to two simultaneous sinusoidal displacements...
Text Solution
|
- Three simle harmionic motions in the same direction having the same am...
Text Solution
|