A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CP SINGH-SIMPLE HARMONIC MOTION-Exercises
- Three simle harmionic motions in the same direction having the same am...
Text Solution
|
- Function x=Asin^2omegat+Bcos^2omegat+Csinomegatcosomegat represents SH...
Text Solution
|
- A particle of mass m oscillates with simple harmonic motion between po...
Text Solution
|
- For a particle executing SHM, the displacement x is given by x = A cos...
Text Solution
|
- A particle of mass m is released from rest and follow a particle part ...
Text Solution
|
- The free and of a simple pendulum is attached to the ceiling of a box....
Text Solution
|
- A body of mass m falls from a height h onto the pan of a spring balanc...
Text Solution
|
- A small block is connected to one end of a massless spring of un - str...
Text Solution
|
- Suppose a tunnel is dug along a diameter of the earth. A particle is d...
Text Solution
|
- A simple pendulum has time period (T1). The point of suspension is now...
Text Solution
|
- A particle of mass (m) is executing oscillations about the origin on t...
Text Solution
|
- A particle oscillating under a force vecF=-kvecx-bvecv is a (k and b a...
Text Solution
|
- The amplitude of a vibrating body situated in a resisting medium
Text Solution
|
- The amplitude of a damped oscillator becomes half in one minutes. The ...
Text Solution
|
- In case of a forced vibration the resonance wave becomes very sharp wh...
Text Solution
|
- A particle with restoring force proportional to displacement and resis...
Text Solution
|
- A weakly damped harmonic oscillator of frequency n1 is driven by an ex...
Text Solution
|
- The amplitude of vibration of a particle is given by am=(a0)//(aomega^...
Text Solution
|
- The equation (d^2y)/(dt^2)+b(dy)/(dt)+omega^2y=0 represents the eq...
Text Solution
|
- The equation of a damped simple harmonic motion is m(d^2x)/(dt^2)+b(dx...
Text Solution
|
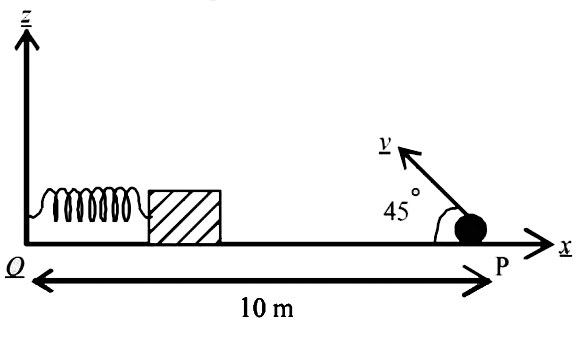 .
.