Home
Class 11
PHYSICS
A mass M is suspended by a weightless st...

A mass `M` is suspended by a weightless string The horizontal force required to hold the mass `60^(@)` with the vertical is .

Text Solution

Verified by Experts

`F = T sin theta -----(1)`
`Mg = T cos theta -----(2)`
Dividing Eq. (1) and Eq. (2)
`(F)/(Mg) = (T sintheta)/(T costheta), F =mg tan theta`
`F =Mg tan 60^(@), F = sqrt3 Mg`
.
Promotional Banner

Topper's Solved these Questions

  • NEWTONS LAWS OF MOTION

    NARAYNA|Exercise C.U.Q|73 Videos

  • NEWTONS LAWS OF MOTION

    NARAYNA|Exercise LEVEL -I (C.W)|47 Videos

  • MOTION IN A STRAIGHT LINE

    NARAYNA|Exercise Level 2 H.W|29 Videos

  • OSCILLATIONS

    NARAYNA|Exercise EXERCISE - IV|41 Videos

Similar Questions

Explore conceptually related problems

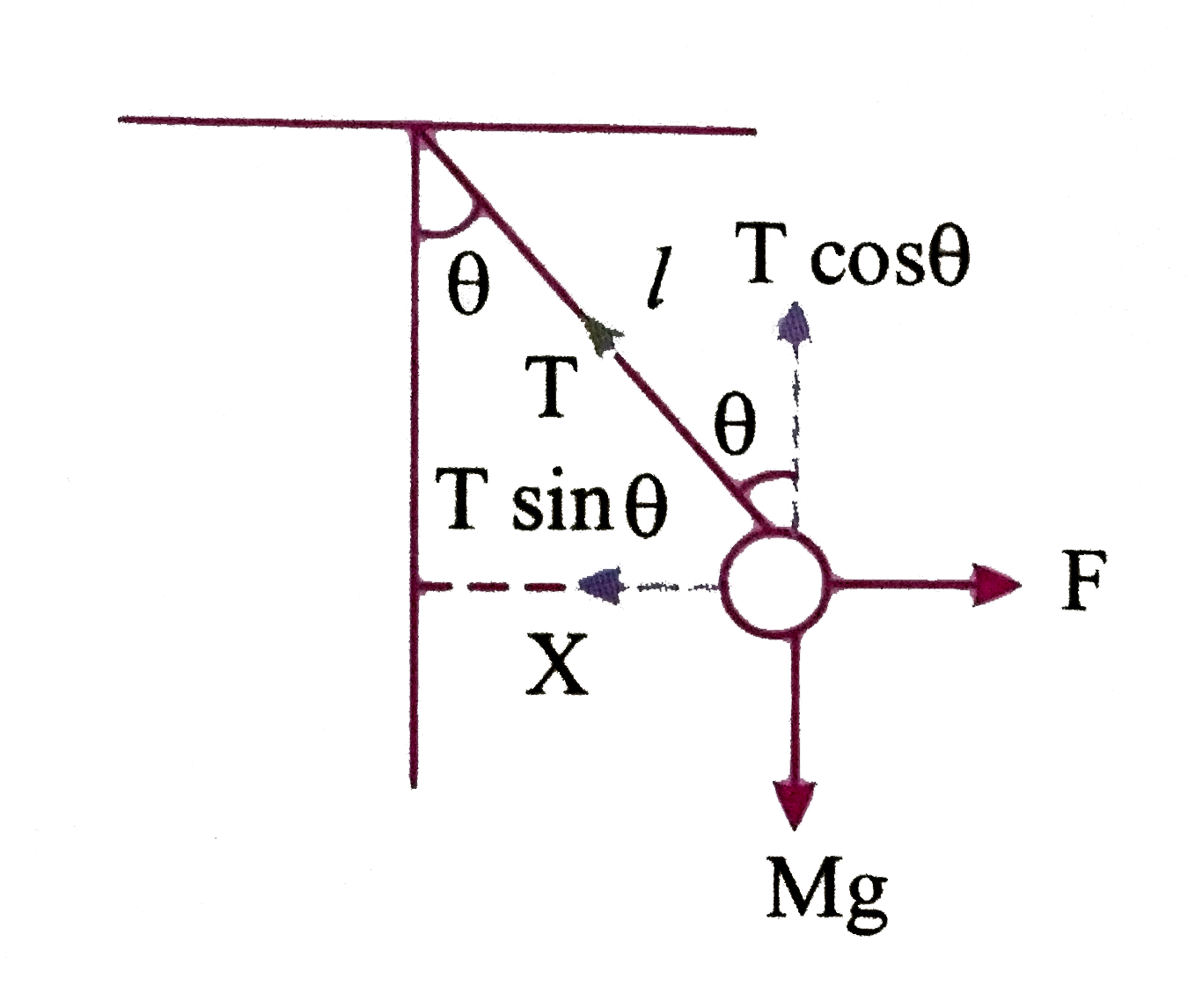
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45^@ with the initial vertical direction is

A particle of mass m suspended by a string of length l revolves in a horizontal circle ( theta is the angle the string makes with vertical). Which of the following statement(s) is // are correct?

A mass m is suspended from a weightless spring. The time period of oscillation of mass is 3 s . Calculate the value of m if on suspending an additional mass of 3kg, time period increases by 2 s.

A body of mass 0.5 kg is suspended by a weightless spring of force constant 500 Nm^(-1) . Another body of mass 0.1 kg moving vertically upwards with velocity of 5 ms^(-1) hits the suspended body and gets embeded into the suspended body. What will be the frequency of oscillation ?

A body of mass 1kg is suspended from a weightless spring having force constant 600N//m . Another body of mass 0.5 kg moving vertically upward hits the suspended body with a velocity of 3.0m//s and get embedded in it. Find the frequency of oscillations and amplitude of motion.

A particle of mass m=2 kg is suspended in a vertical plane by two strings - one horizontal and the other inclined to the vertical by alpha = 30^(@) . Find the tension of the inclined string (a) an instant before the horizontal one is cut, (b) an instant after the horizontal one is cut.