Home
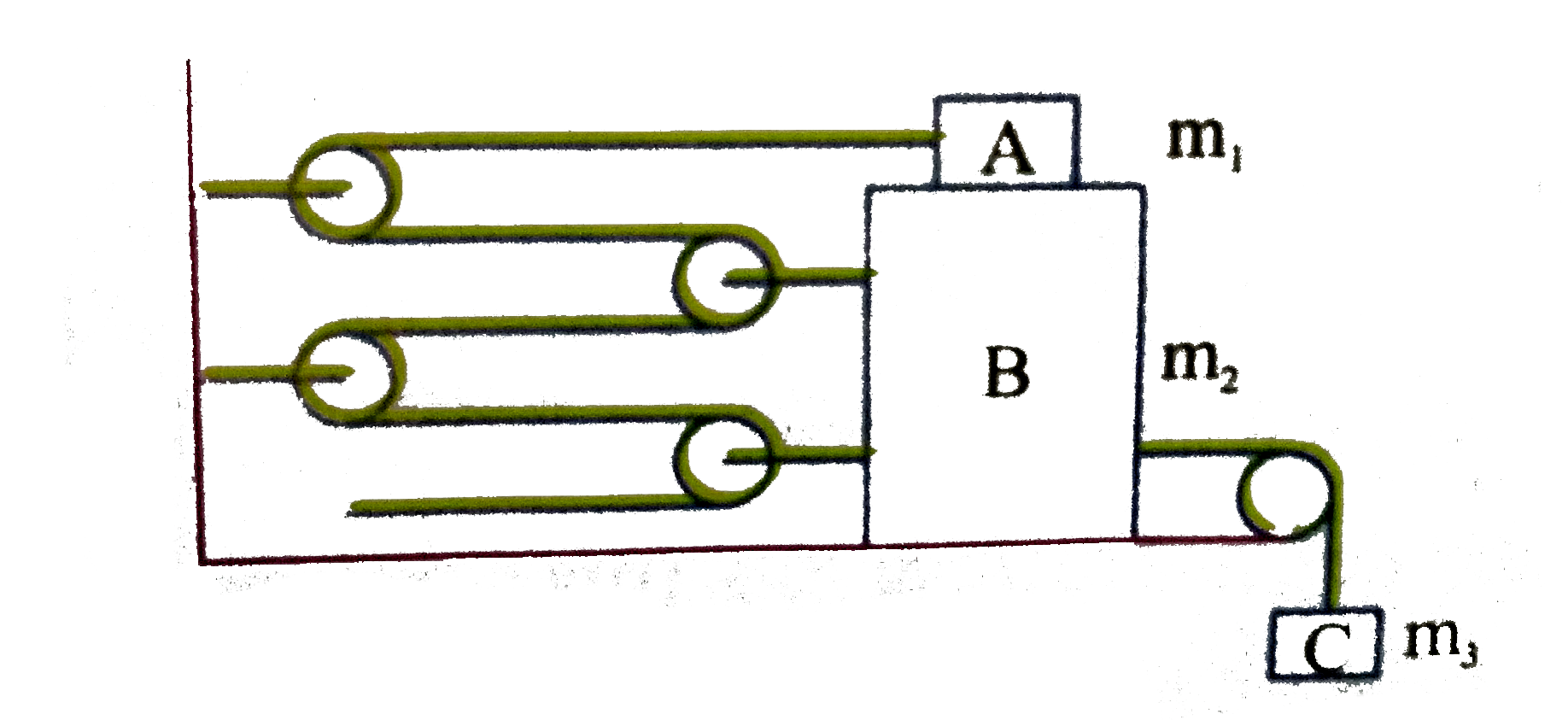
Class 11
PHYSICS
In the figure, m(1)=m(2)=10 kg. The coef...

In the figure, `m_(1)=m_(2)=10 kg`. The coefficients of friction between `A, B` and `B`, surface are `0.2`. Find the maximum value of `m_(3)` so that no block slips ( All the pullies are ideal and strings are massless).

A

`16 kg`

B

`10 kg`

C

`18 kg`

D

`14 kg`

Text Solution

Verified by Experts

The correct Answer is:
D

`(f_(2))_("lim")=*(m_(1)+m_(2))g=0.2xx20xx10=40N`
`T^(1)=m_(3)g` and `T^(1)=f_(1)+f_(2)+4T`
`rArrm_(3)(10)=20+40+4(20)rArrm_(3)=14 kg`
Promotional Banner

Topper's Solved these Questions

  • FRICTION

    NARAYNA|Exercise Multiple answer question|20 Videos

  • FRICTION

    NARAYNA|Exercise Passage type of questions|6 Videos

  • COLLISION

    NARAYNA|Exercise Level-II (H.W)|54 Videos

  • GRAVITATION

    NARAYNA|Exercise EXERCISE -IV|40 Videos

Similar Questions

Explore conceptually related problems

1 kg and 4 kg blocks lie on a rough horizontal surface. The coefficient of friction between 4 kg blocks and surface is 0.2 while the coefficient of firction between 1 kg blocks and the surface is 0.6 . All the pulley shown in the figure are massless and frictionless and all strings are massless and frictionless and all strings are massless.

In the figure m_(A) = m_(B) = m_(C) = 60 kg . The coefficient of friction between C and ground is 0.5 B and ground is 0.3, A and B is 0.4. C is pulling the string with the maximum possible force without moving. Then the tension in the string connected to A will be

Three blocks A , B and C , whose masses are 9kg , 9kg and 18kg respectively as shown in the figure, are released from rest. The co-efficient of friction between block A and the horizontal surface is 0.5 & the co-efficient of friction between block B and the horizontal surface is 0.5 . Find the acceleration of block C just release [Take g=10m//s^(2) ]. All strings and pulleys are ideal

Two blocks A and B of masses m_(A) = 1kg and m_(B) = 3kg are kept on the table as shown in figure. The coefficient of friction between A and B is 0.2 and between B and the surface of the table is also 0.2. The maximum force F that can be applied on B horizontally, so that the block A does not slide over the block B is ________ (in N): [Take g = 10 m//s^(2) ]

In the figure shown m_(1)=5 kg,m_(2) = 10 kg & friction coefficient between m_(1) & m_(2) is mu=0.1 and ground is frictionless then :

Consider three blocks placed one over the other as shown in Fig. Let as now pull the blocks with the force of magnitudes 18 N, 100 N and 15 N Take m_(1) = m_(2) = m_(3) = 10 kg If the coefficient of static and kinetic friction between all contacting surface are mu_(g) = 0.2 respectively find the (a) Acceleration of the block s (b) Friction at each surface

There block A B ,and C of equal mass m are placed one over the other on a frictionless surface (table) as shown in figure The coefficient of friction between any blocks A ,B and C is mu The maximum value of mass of block D so that the blocks A,B and C move without slipping over each other is

Two masses m_(1) =10 Kg and m_(2)=5kg are connected by an ideal string as shown in the figure. The coefficient of friction between m_(1) and the surface is mu=0.2 Assuming that the system is released from rest calculate the velocity of blocks when m_(2) has descended by 4m . (g=10 m//s^(2)) .

A block of mass m_(1) connected with another of mass m_(2) by a light spring of natural length l_(0) and stiiffness k is kept stationary on a rough horizontal surface . The coefficient of friction between m_(1) and surface is mu and the block m_(2) is smooth .The block m_(2) is moved with certain the block m_(1) in horizontal plane Find the (a) maximum to m_(1) and (b) acceleration of m_(2) in part(a)

The coefficient of static friction, mu_(s) between block A mass 2kg and the table as shown in the figure, is 0.2. What would be the maximum mass value of block B, so that the two blocks do not move ? The string and the pulley are asseumed to be smooth and massless ( g=10m//s^(2) )