Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NARAYNA-SYSTEM OF PARTICLES-Level-VI
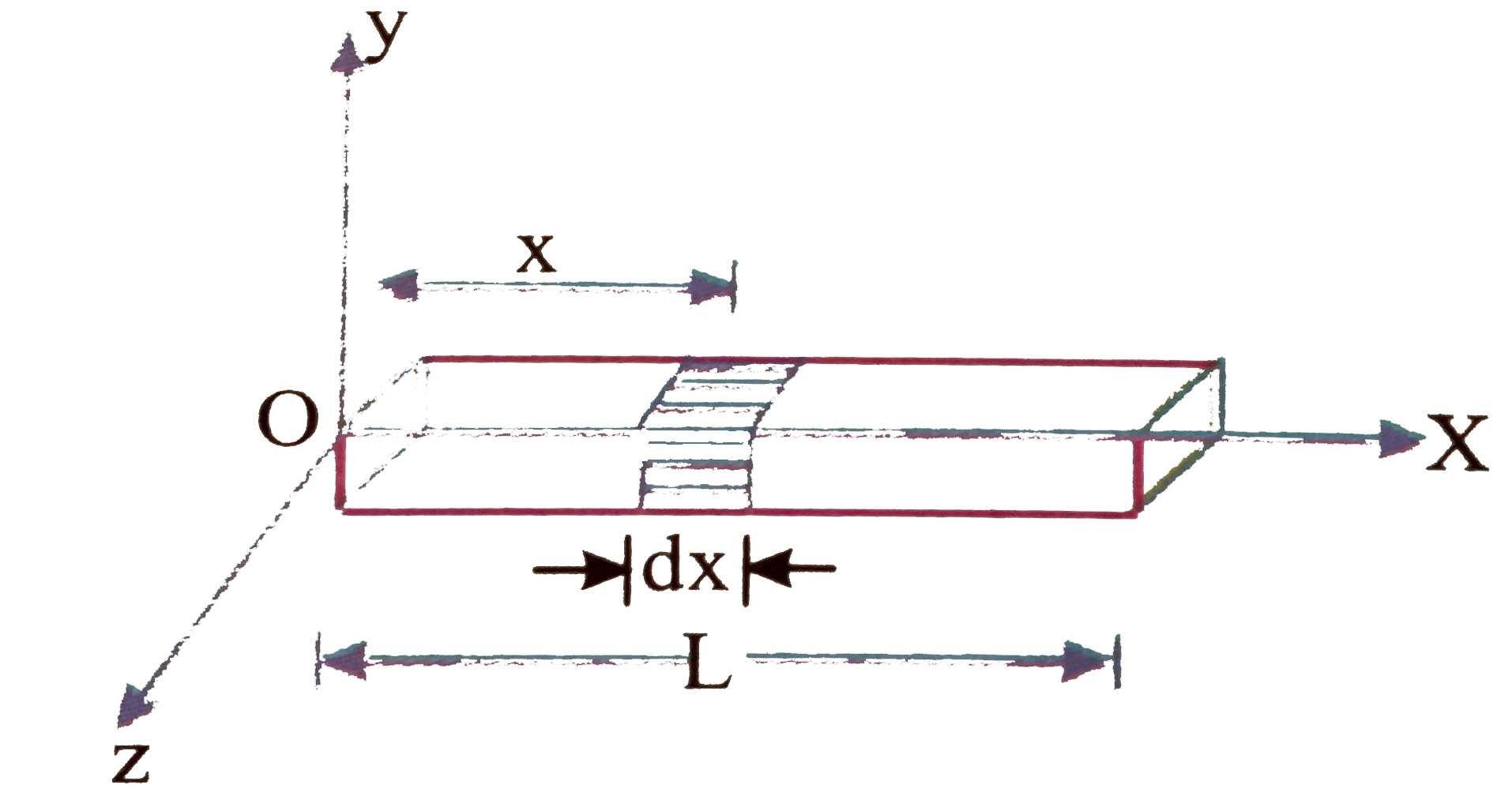
- The density of a linear rod of length L varies as rho=A+Bx where x is ...
Text Solution
|
- The point P of a string is pulled up with an acceleration g. Then the ...
Text Solution
|
- A plank of mass M is placed over smooth inclined plane and sphere is a...
Text Solution
|
- Four beads each of mass m are glued at the top, bottom and the ends of...
Text Solution
|
- A rolling body is connected with a trolley car by a spring of stiffne...
Text Solution
|
- A linear impulse int Fdt acts at a point C of the smooth rod AB. The v...
Text Solution
|
- Two light vertical springs with equal natural length and spring consta...
Text Solution
|
- Ler l be the moment of inertia of a uniform square plate about an axi...
Text Solution
|
- Two point masses A of mass M and B of mass of 4M are fixed at the ends...
Text Solution
|
- A conical pendulum consists of a mass M suspended from a string of len...
Text Solution
|
- A ring of mass m and radius R is rolling down on a rough inclined plan...
Text Solution
|
- A ring of mass M and radius R lies in x-y plane with its centre at ori...
Text Solution
|
- As shown in figure, the hinges A and B hold a uniform 400N door in pla...
Text Solution
|
- Find minimum height of the obstacle so that the shpere can stay in equ...
Text Solution
|
- In the figure shown, suppose the compound pulley and the disc have the...
Text Solution
|
- Two identical rings A and B are acted upon by torques tau(A) and tau(B...
Text Solution
|
- A uniform solid sphere of radius r is rolling on a smooth horizontal s...
Text Solution
|
- Angular acceleration of the cylinder C shows in the figure is (all str...
Text Solution
|
- A particle of mass m is released from rest at point A in the figure fa...
Text Solution
|
- The end B of the rod AB which makes angle theta with the floor is bein...
Text Solution
|
- A block having equilateral triangular cross-section of side a and mass...
Text Solution
|