Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
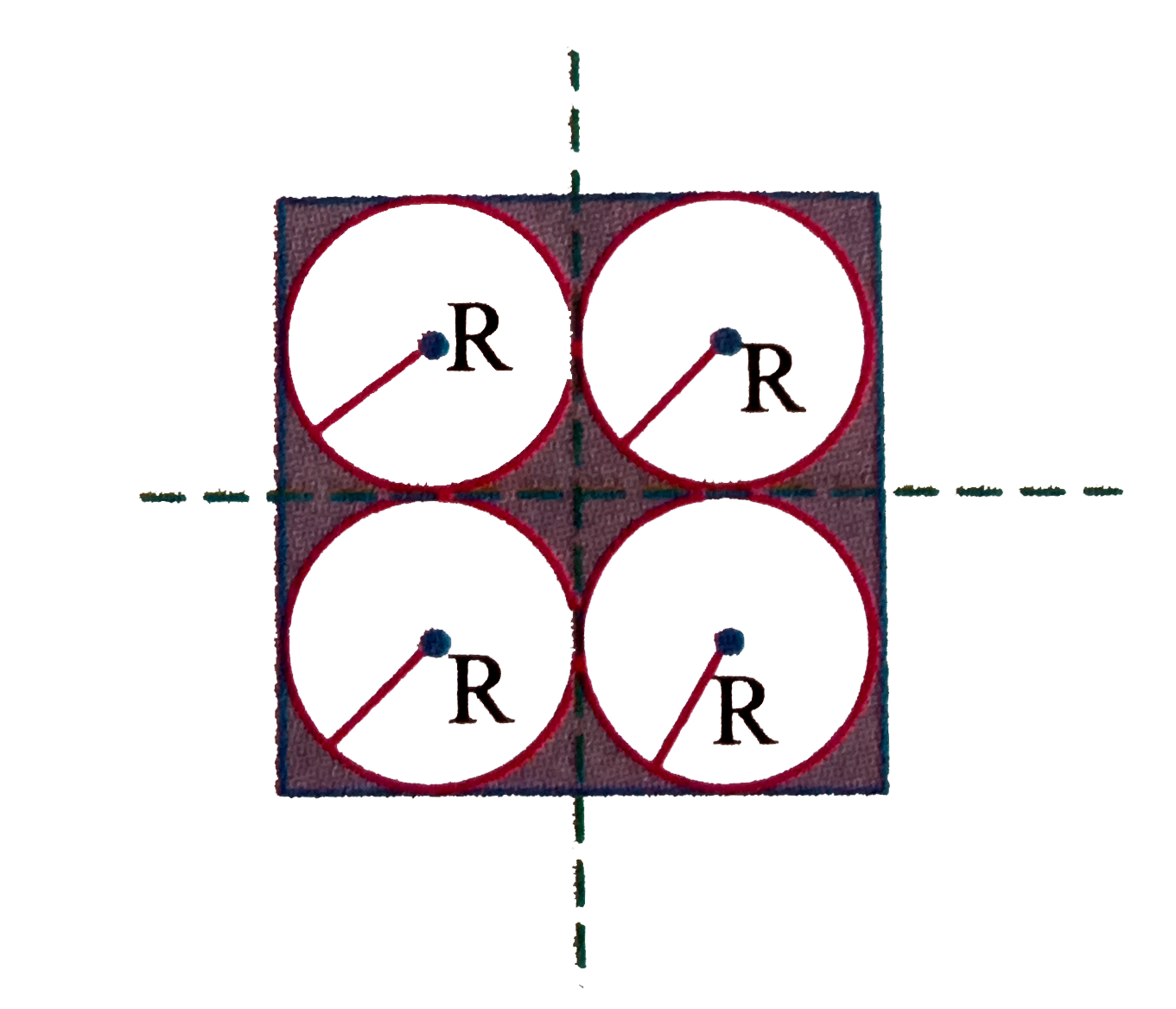
- Four holes of radius R are cut from a thin square plate of side 4 R an...
Text Solution
|
- From a uniform square plate of side a and mass m , a square portion DE...
Text Solution
|
- Four holes of radius R are cut from a thin square plate of side 4 R an...
Text Solution
|
- From a disc of radius R and mass M , a circular hole of diameter R , w...
Text Solution
|
- A hole of radius R/2 is cut from a thin circular plate of raduis R as ...
Text Solution
|
- A concentric hole of radius R/2 is cut from a thin circular plate of ...
Text Solution
|
- A hole of radius R//2 is removed from a thin circular plate of radius ...
Text Solution
|
- एक 4R भुजा व M द्रव्यमान वाले वर्ग में 4 छिद्र जिनकी त्रिज्या R है, चि...
Text Solution
|
- M द्रव्यमान व 4R भुजा वाली वर्गाकार पट्टिका से R त्रिज्या वाले 4 छिद्र...
Text Solution
|
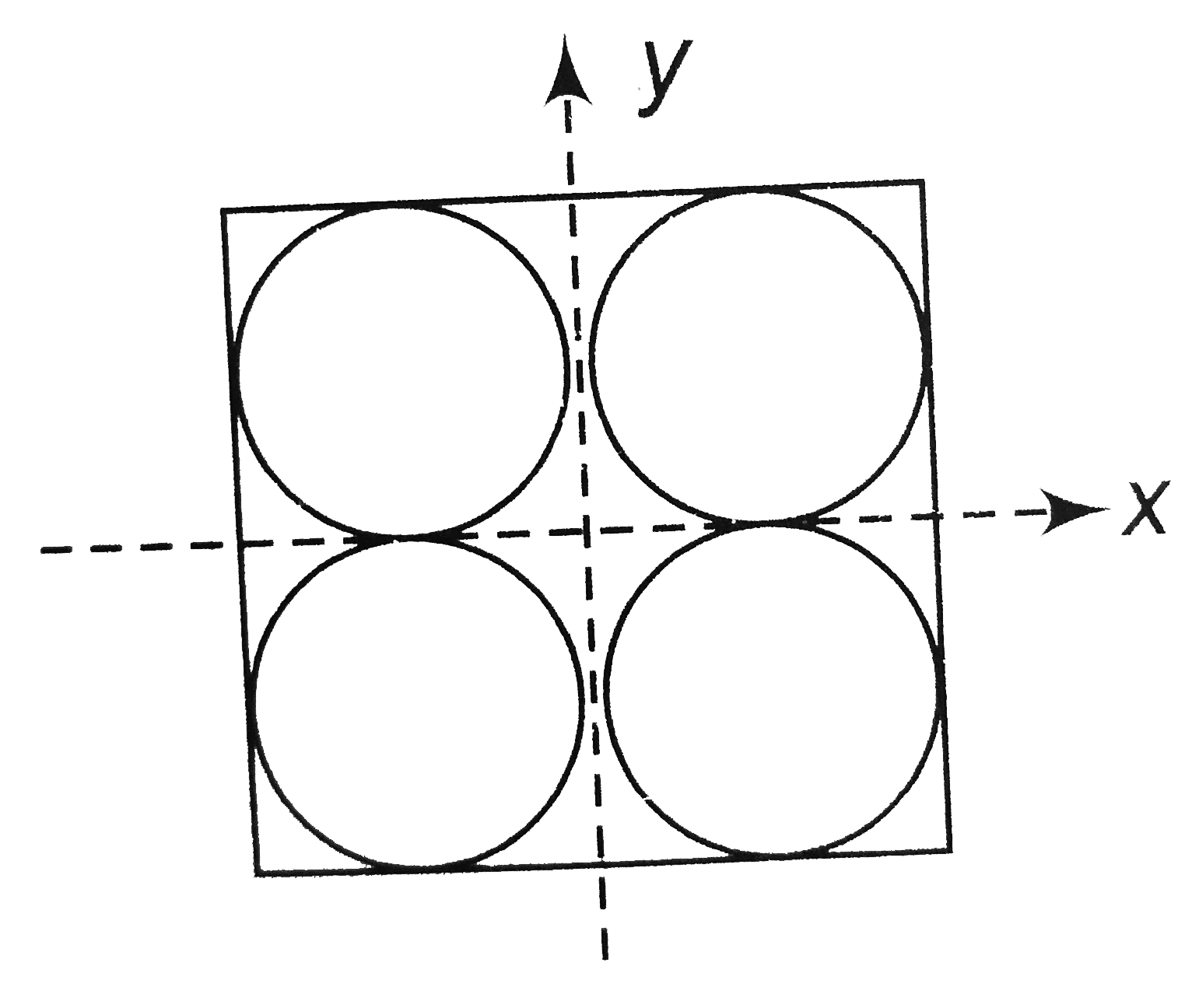 .
.