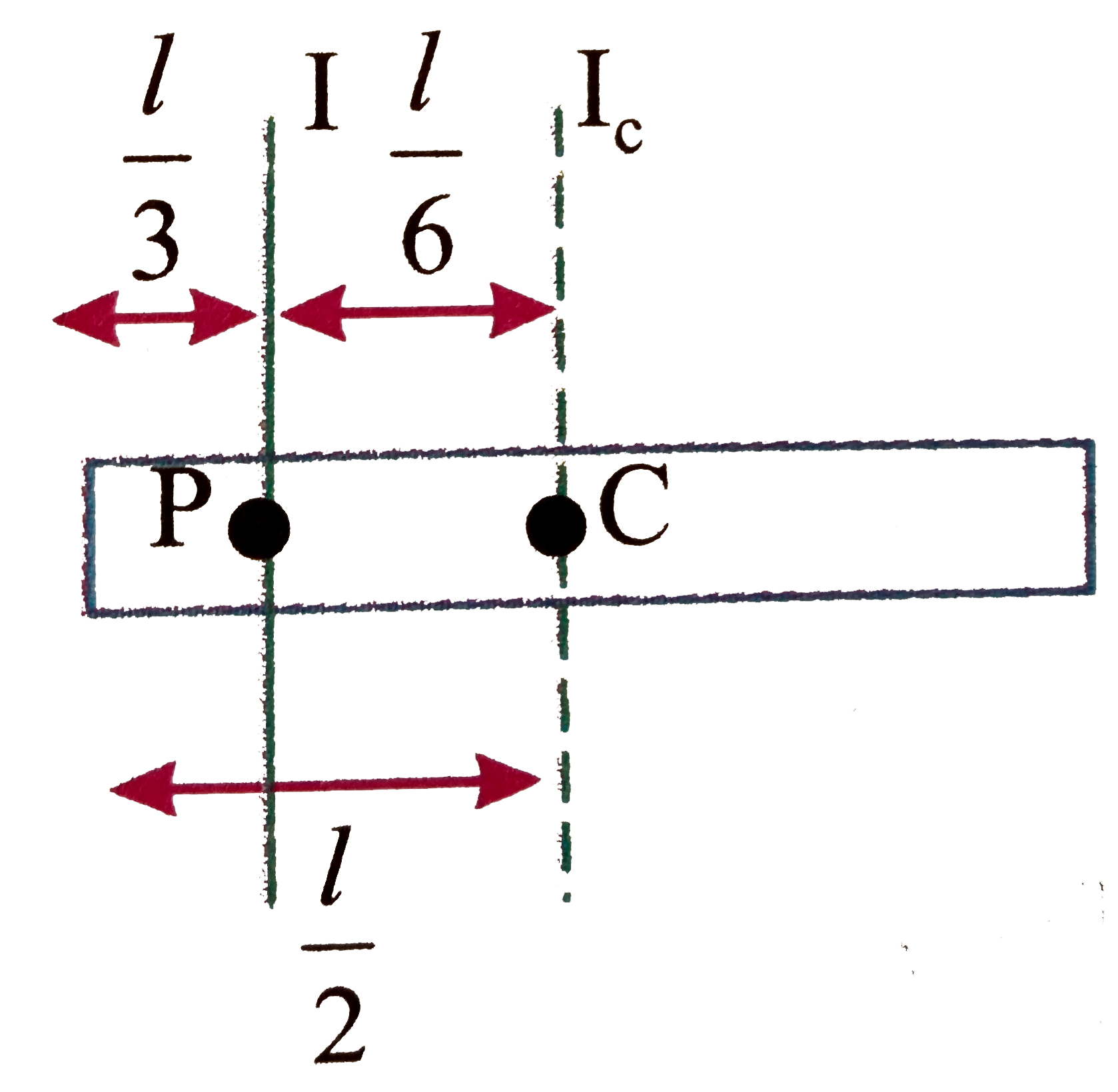
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the moment of inertia of a thin uniform rod about an axis perpend...
Text Solution
|
- The radius of gyration of an uniform rod of length l about an axis pas...
Text Solution
|
- Find the radius of gyrational and moment of inertia of a rod of mass 1...
Text Solution
|
- Find the moment of inertia of a thin uniform rod about an axis perpend...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- The moment of inertia of a thin uniform rod about an axis passing thro...
Text Solution
|
- Moment of inertia of a thin uniform rod about an axis passing through ...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- Derive an expression for the moment of inertia of thin uniform rod abo...
Text Solution
|