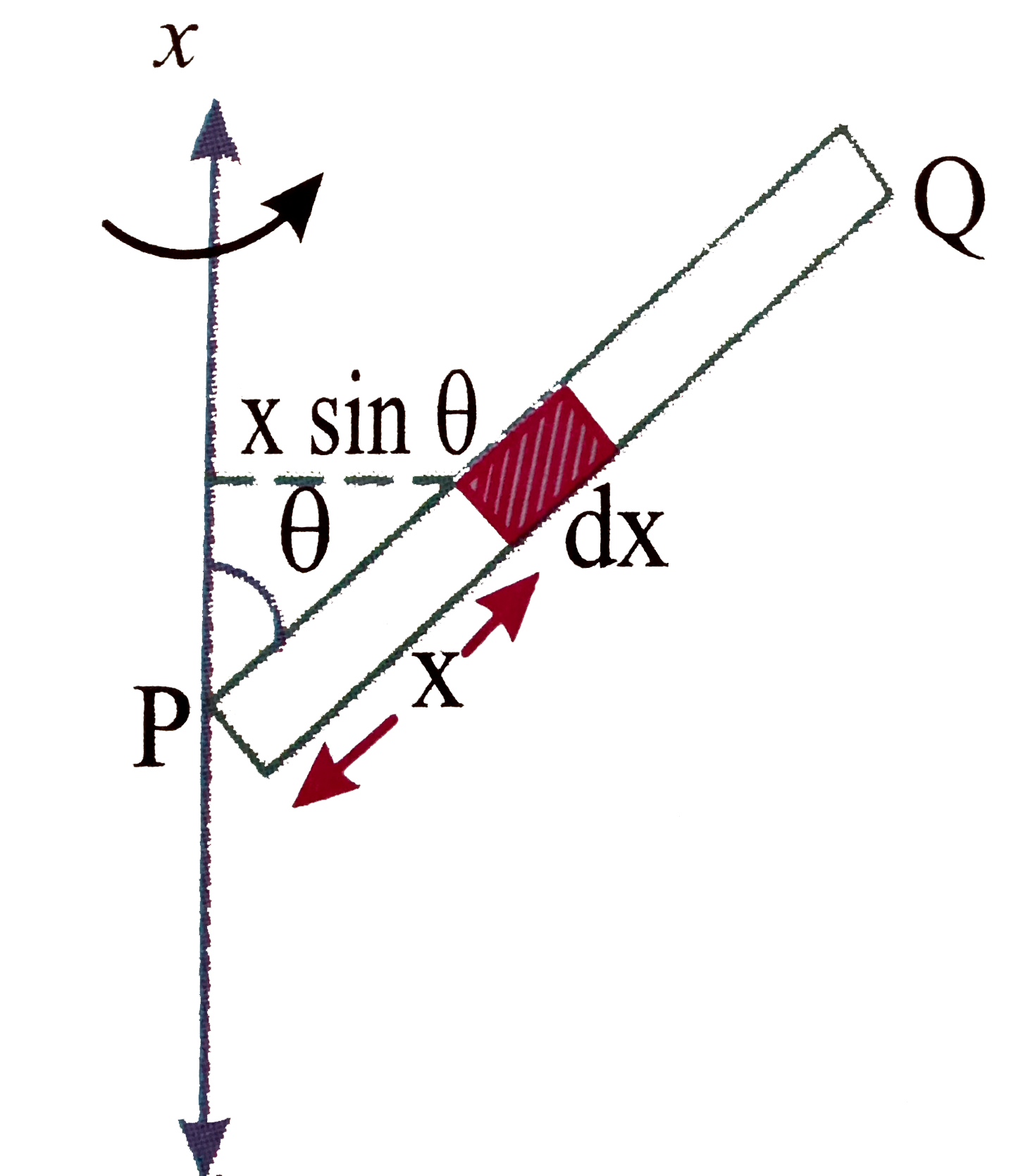
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the moment of inertia of the rod AB about an axis yy as shown in ...
Text Solution
|
- Find the moment of inertia of the rod AB about an axis yy as shown in ...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- The moment of inertia of a thin rod of mass M and length L about an ax...
Text Solution
|
- Calculate the moment of inertia of a thin rod of mass m and length l a...
Text Solution
|
- The moment of inertia of a system of four rods each of length l and m...
Text Solution
|
- The moment of inertia of a thing uniform rod of length L and mass M , ...
Text Solution
|
- किसी पतली छड़ (द्रव्यमान M, लम्बाई L) का इसकी लम्बाई के लम्बवत् सिर...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|