Home
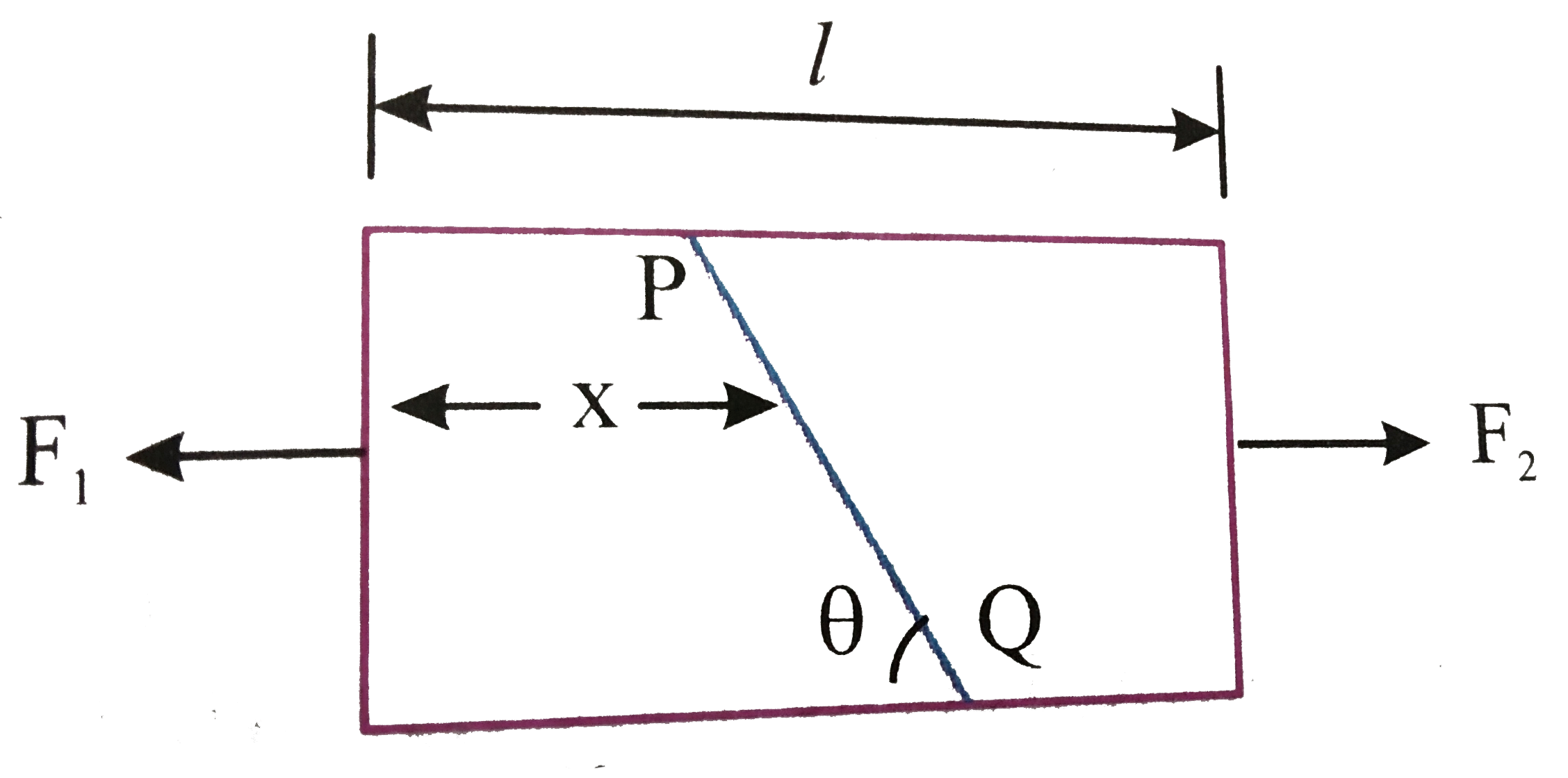
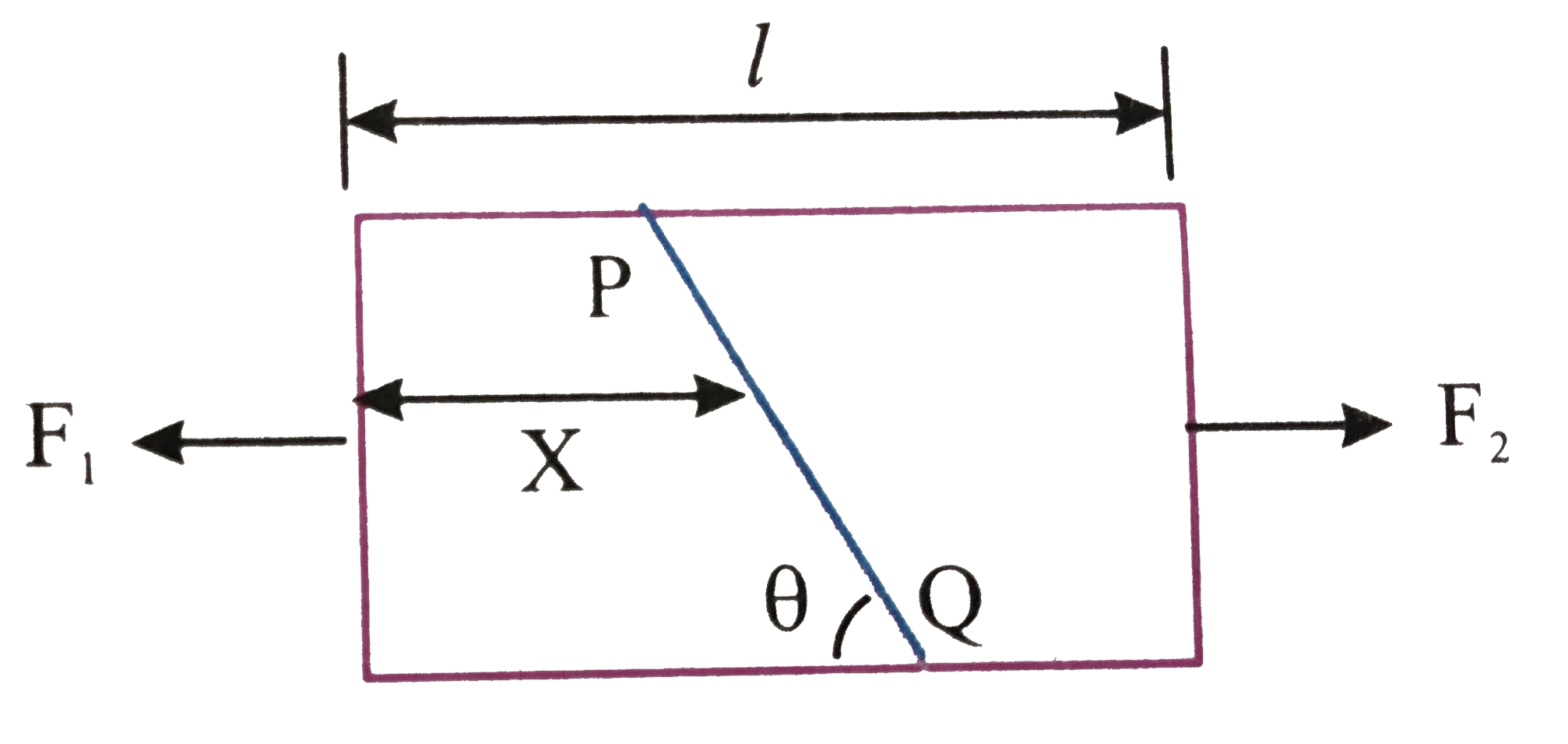
Class 11
PHYSICS
Two forces F(1) and F(2) are applied at...

Two forces `F_(1)` and `F_(2)` are applied at the ends of a metal rod of Yougn's Modulus `Y`, length `l` as shown.

Longitudinal stress at the given cross-section `PQ` if the cross-section of the rod is `A_(0)` and tension is `T`

A

`(T sin^(2) theta)/(A_(0))`

B

`(T sin theta)/(A_(0))`

C

`(T sin theta)/(2A_(0))`

D

`(2T sin theta)/(2A_(0))`

Text Solution

Verified by Experts

The correct Answer is:
A

Tension at a distance `x` is given by
`(F_(1) - (F_(1) - F_(2)) (x)/(l))`
Shearing stress `= (T cos theta )/(a// sin theta) = (T sin^(2) theta)/(A_(0))`
where `T = (F_(1) - (F_(1) - F_(2))(x)/(l))`
Promotional Banner

Topper's Solved these Questions

  • MECHANICAL PROPERTIES OF SOLIDS

    NARAYNA|Exercise SINGLE ANSWER TYPE QUESTIONS|13 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    NARAYNA|Exercise Comprehension-1:|2 Videos

  • MECHANICAL PROPERTIES OF SOLIDS

    NARAYNA|Exercise MULTIPLE ANSWER TYPE|10 Videos

  • MECHANICAL PROPERTIES OF FLUIDS

    NARAYNA|Exercise EXERCISE - III|30 Videos

  • MOTION IN A PLANE

    NARAYNA|Exercise Level-II(H.W)|31 Videos

Similar Questions

Explore conceptually related problems

A homogeneous rod of length L is acted upon by two forces F_(1) and F_(2) applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F_(1) is applied?

Two forces F_(1) and F_(2) ( F_2 gt F_(1)) are applied at the free ends of uniform rod kept on a horizontal frictionless surface. Find tension in rod at a distance x from end ‘A’,

A force F doubles the length of wire of cross-section a The Young modulus of wire is

on heating a cylindrical metallic rod, its length increases by 2% . Then area of cross section of rod will

Two equal and opposite point forces applied at mid- points of the ends of a rod of square cross shown. Consider the dotted section ABCD . If the rod is cut across this Gloss section, the force exerted by the right part of the rod on left part across this cross section is

A uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is

A rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

Two equal and opposite forces F and -F act on a rod of unifrom cross-sectional ara A , as shown in the figure. Find the (i) shearing (ii) longitual stress on the section AB .

Two point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be