Home
Class 12
PHYSICS
A ball of mass (m) 0.5 kg is attached to...

A ball of mass `(m) 0.5 kg` is attached to the end of a string having length `(L) 0.5 m`. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is `324 N`. The maximum possible value of angular velocity of ball (in radian//s) is -
.

A

`9`

B

18

C

27

D

36

Text Solution

Verified by Experts

The correct Answer is:
D
The tension is resolved into horizontal copmponent T ` sin theta ` and vertical component `T cos theta `. ` T sin theta ` provides the centripetal force required for the horizontal circular motion

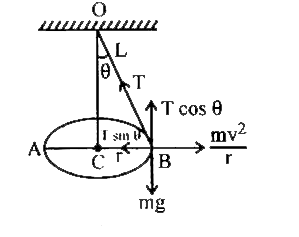
`therefore T sin theta = (mv^(2))/(r ) = m r omega ^(2)`
From the figure ` sin theta = (BC)/(OB) =(r )/(L )`
` therefore T. (r )/(L ) = m r omega ^(2) therefore T= Lomega ^(2)`
` omega^(2) = (T )/(mL ) = (324 )/((1)/(2)xx(1)/(2) )=324 xx4`
` therefore omega = sqrt(324xx4)=18 xx2=36 rad //s`
Promotional Banner

Topper's Solved these Questions

  • CIRCULAR MOTION

    MARVEL PUBLICATION|Exercise TEST YOUR GRASP-1|1 Videos

  • CIRCULAR MOTION

    MARVEL PUBLICATION|Exercise TEST YOUR GRASP-2|1 Videos

  • ATOMS, MOLECULES AND NUCLEI

    MARVEL PUBLICATION|Exercise TEST YOUR GRASP|30 Videos

  • COMMUNICATION SYSTEMS

    MARVEL PUBLICATION|Exercise TEST YOUR GRASP -20|10 Videos

Similar Questions

Explore conceptually related problems

A ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is

A ball of mass m = 0.5 kg is attached to the end of a string having length L = 0.5 is rotated on a horizontal circular path about the vertical axis. The maximum tension that the string can bear is 324N.What is the maximum possible value of angular velocity of ball ( in radian // s ) ?

A bob of mass 0.25 kg is attached with a string of length 0.25 m . The bob is rotated on a horizontal circle. The maximum tension that string can bear is 225 N . Maximum possible value of angular velocity of bob (in rad/s) is :

A stone of mass 0.5kg is attached to a string of length 2m and is whirled in a horizontal circle. If the string can withstand a tension of 9N the maximum velcoity with which the stone can be whirled is .

A ball of mass 0.25 kg attached to the end of a string of length 1.96 m is moving in a horizontal circle. The string will break if the tension is more than 25 N . What is the maximum speed with which the ball can be moved

A ball of mass 0.25kg attached to the ends of a string of length 1.96m is rotating in a horizonal circle. The string will break, If tension is more than 25N. What is the maximum velocity with which the ball can be rotated ?

A ball of mass 0.25kg attached to the end of a string of length 1.96m moving in a horizontal circle. The string will break if the tension is more than 25N . What is the maximum speed with which the ball can be moved.

A string breaks under a load of 4.8kg A mass of 0.5 kg is attached to one end of a string 2 m long and is rotated in a horizontal circle. Calculate the greatest number of revolutions that the mass can make without breaking the string.