A particle of mass m is rotated in a vertical circle by means of a string . The differnce in the tensions in the string at the bottom and the top of the circle would be

Options

A. 2 mg
B. 3 mg
C. 4mg
D. 6 mg

Answer

D

Explanation

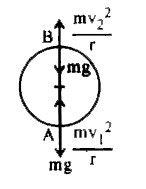
when the body is at A , there is maximum tension in the string .
`T_(max) =(mv_(1)^(2))/(r ) + mg ` and when it is at B , the tension in the string is minimum
and `T_(min ) = ( mv_(2)^(2))/( r ) - mg `
` therefore T_(max) - T_(min ) - ( m) /(r ) ( v_(1) ^(2)- v_(2)^(2)) + mg -(-mg)`
But for completing the vertical circle
`V_(1) - sqrt( 5 gr ) and v_(2)= sqrt( gr)`
` therefore (m ) /(r ) (v_(1)^(2)- v_(2)^(2) ) = (m ) /(r ) [ 5 gr - gr] = 4 mg `
` therefore T_(max) - T_(min) = 4 mg + 2mg = 6 mg `