Home
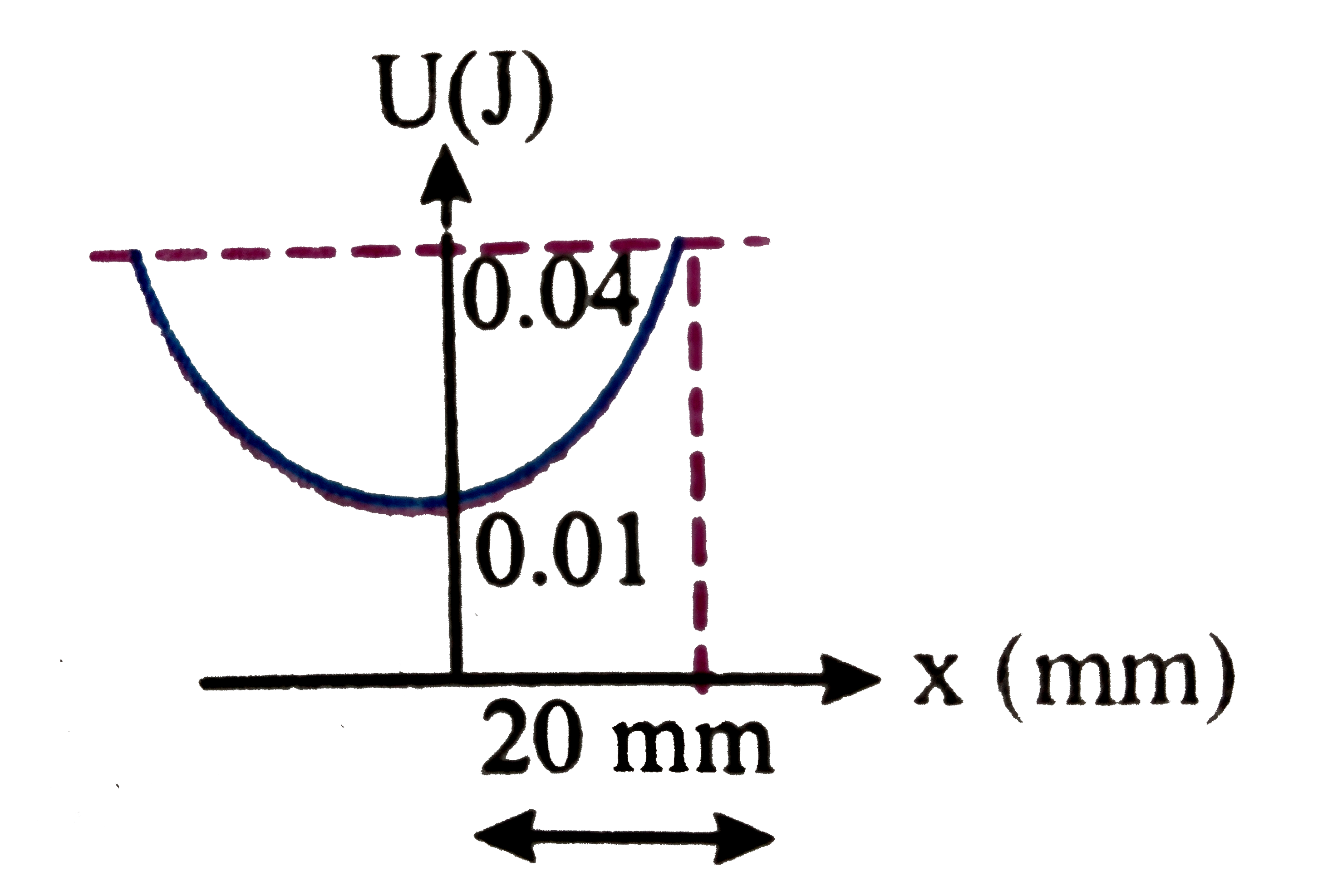
Class 11
PHYSICS
The variation of potential energy (U) of...

The variation of potential energy `(U)` of a simple harmonic oscillator is as shown. Then force constant of the system is `(PE` is in joules, displacement 'x' is in mm)

A

`100N//m`

B

`150 N//m`

C

`(200)/(3)N//m`

D

`300N//m`

Text Solution

Verified by Experts

The correct Answer is:
B
`DeltaU = (1)/(2)KA^(2)`
Promotional Banner

Topper's Solved these Questions

  • OSCILLATIONS

    NARAYNA|Exercise NCERT BASED QUESTIONS|1 Videos

  • OSCILLATIONS

    NARAYNA|Exercise MULTIPLE ANSWER QUESTIONS|23 Videos

  • OSCILLATIONS

    NARAYNA|Exercise LEVEL -II (C.W)|36 Videos

  • NEWTONS LAWS OF MOTION

    NARAYNA|Exercise PASSAGE TYPE QUESTION|6 Videos

  • PHYSICAL WORLD

    NARAYNA|Exercise C.U.Q|10 Videos

Similar Questions

Explore conceptually related problems

The veriation of potential energy of harmonic escillator is as shown in figure. The spring constant is

The variation of the potential energy of harmonic oscillator is as shown in the figure. The spring constant is

The variation of potential energy U of a system is shown in figure. The force acting on the system is best represented by

The maximum potential energy of a simple harmonic oscilator is U_("max") . The the P.E. of the oscillator when it is half way to its end point is

The energy of a simple harmonic oscillator in the state of rest is 3 Joules. If its mean K.E. is 4 joules, its total energy will be :

If the total energy of a simple harmonic oscillator is E, then its potential energy, when it is halfway to its endpoint will be

Draw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.

If the frequency of the acceleration of a simple harmonic oscillator if (f_0) then the frequency of the potential energy is

NARAYNA-OSCILLATIONS-LEVEL -III
  1. A particle of mass 4g is in a gravitational potential V =(800x^(2) +15...

    Text Solution

    |

  2. A particle free to move along the (x - axis) hsd potential energy give...

    Text Solution

    |

  3. The variation of potential energy (U) of a simple harmonic oscillator ...

    Text Solution

    |

  4. A mass of 0.98 kg suspended using a spring of constant K = 300 Nm^(-1)...

    Text Solution

    |

  5. A small block is connected to one end of a massless spring of un - str...

    Text Solution

    |

  6. The mass (M) shown in the figure oscillates in simple harmonic motion ...

    Text Solution

    |

  7. A block (B) is attached to two unstriched sprig S(1) and S(2) with spr...

    Text Solution

    |

  8. A spring is loaded with two blocks m(1) and m(2) where m(1) is rigidly...

    Text Solution

    |

  9. A body of mass m is released from a height h to a scale pan hung from ...

    Text Solution

    |

  10. A block P of mass m is placed on horizontal frictionless plane. A seco...

    Text Solution

    |

  11. With the assumption of no slipping, determine the mass m of the block ...

    Text Solution

    |

  12. There is a spring with netural length L(0). Two masses m(1) and m(2) a...

    Text Solution

    |

  13. A pendulum of mass m and length L is connected to a spring as shown in...

    Text Solution

    |

  14. A small block is connected to a massless rod, which in turns attached ...

    Text Solution

    |

  15. In the device shown in Fig, the block m is displaced down slightly and...

    Text Solution

    |

  16. A tray of mass 12 kg is supported by two identical springs as shown in...

    Text Solution

    |

  17. A particle of mass 'm' is attached to three identical springs A,B and ...

    Text Solution

    |

  18. One end of a spring of force constant k is fixed to a vertical wall an...

    Text Solution

    |

  19. A simple pendulum of length 4.9m is immersed in a liquid of density rh...

    Text Solution

    |

  20. A simple pendulum is hanging from a peginserted in a vertical wall. It...

    Text Solution

    |