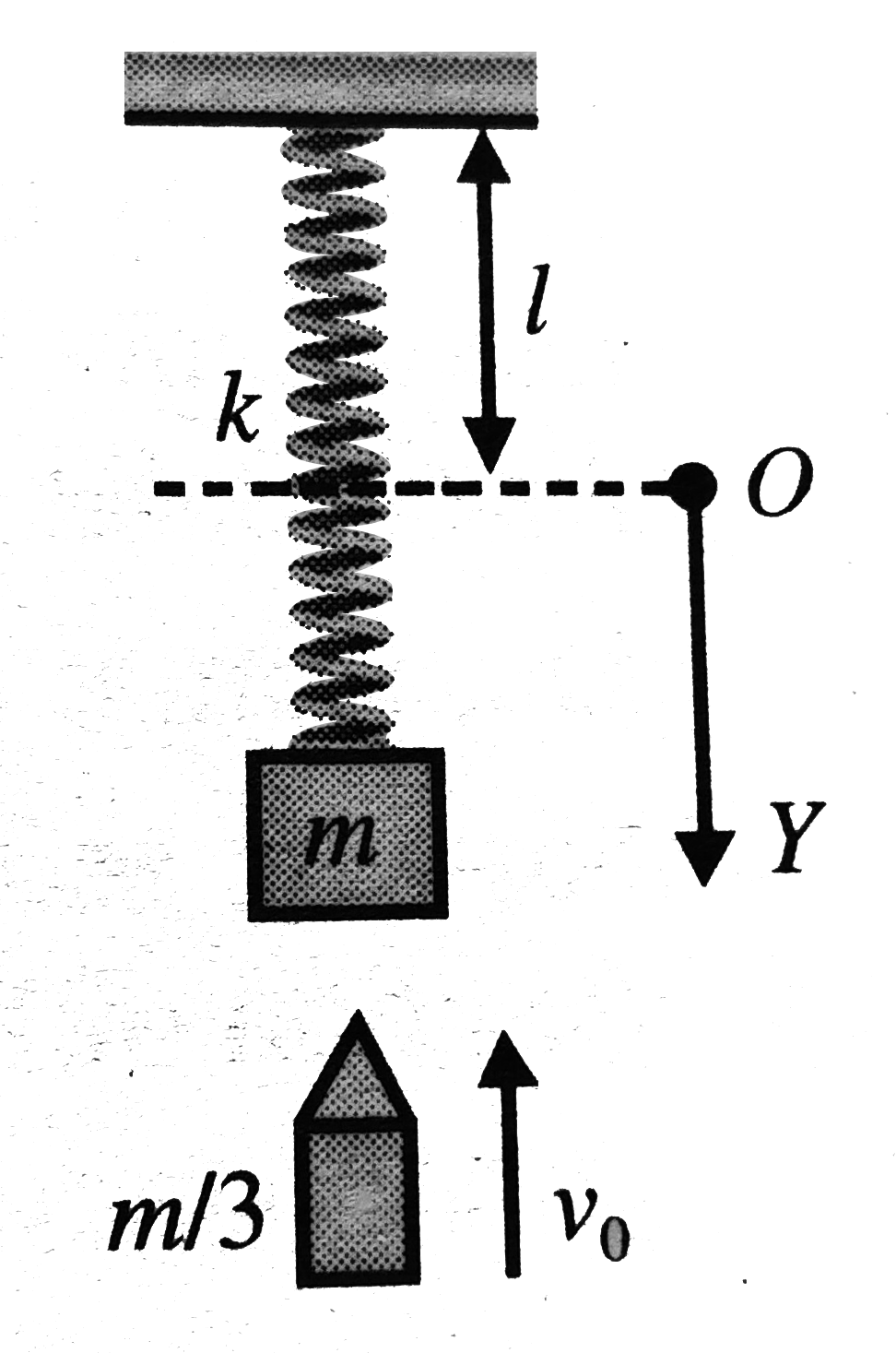
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass `(m)/(3)` moving in vertical up wards direction with velocity `v_0` strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. Mark out the correct statements (s).
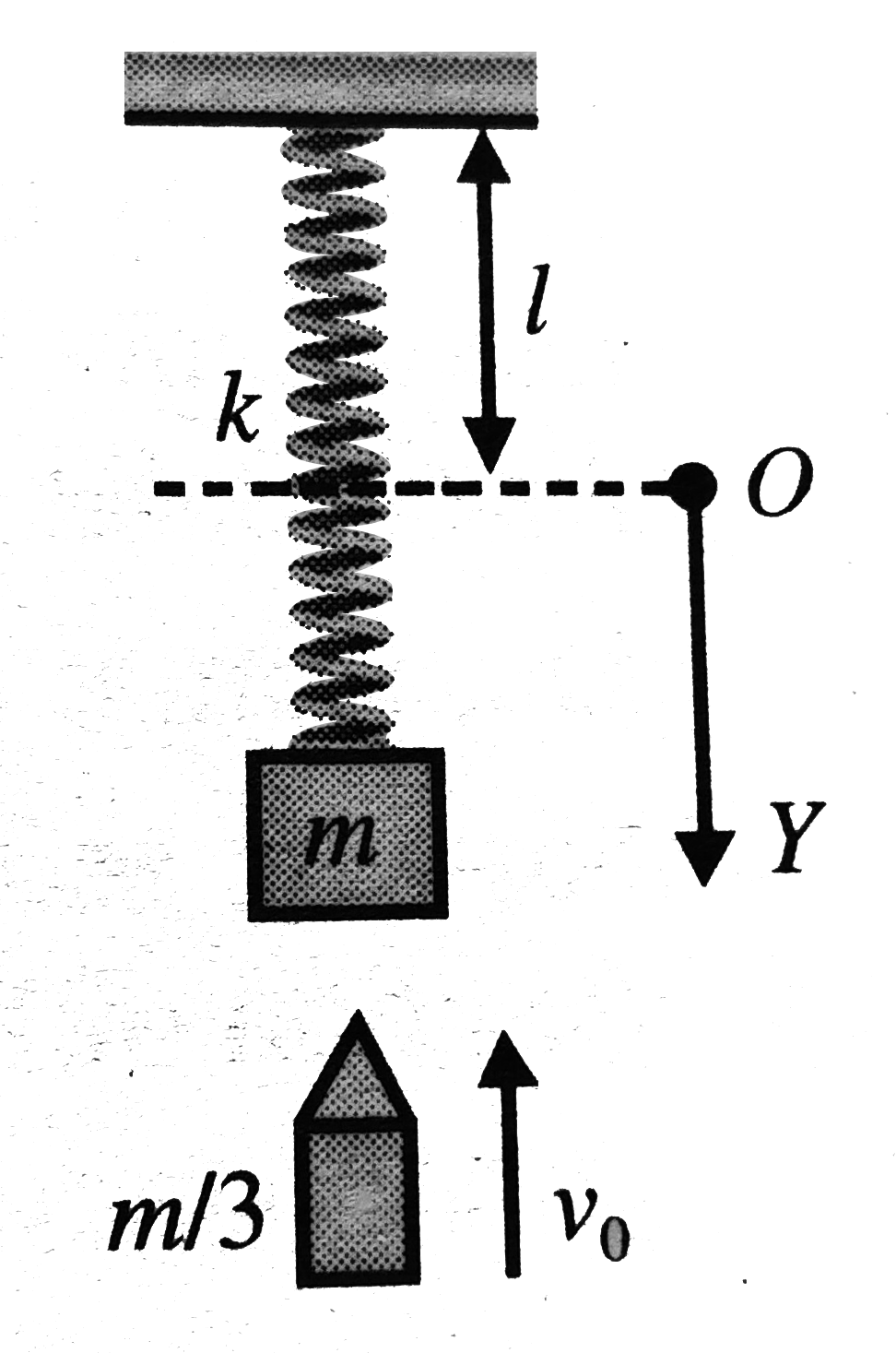
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass `(m)/(3)` moving in vertical up wards direction with velocity `v_0` strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. Mark out the correct statements (s).
A
The block-bullet system performs `S.H.M.` about `y = (mg)/(k)`
B
The block-bullet system performs oscillatory motion but not `S.H.M.` about `y = (mg)/(k)`
C
The block-bullet system performs `S.H.M.` about `y = (4mg)/(3k)`
D
The block-bullet system performs oscillatory motion but not `S.H.M.` about `y = (4mg)/(3k)`
Text Solution
Verified by Experts
The correct Answer is:
C
Initially in equilibrium let the elongation in spring by `y_(0)`, then `rArr y_(0) = (mg)/(k)`
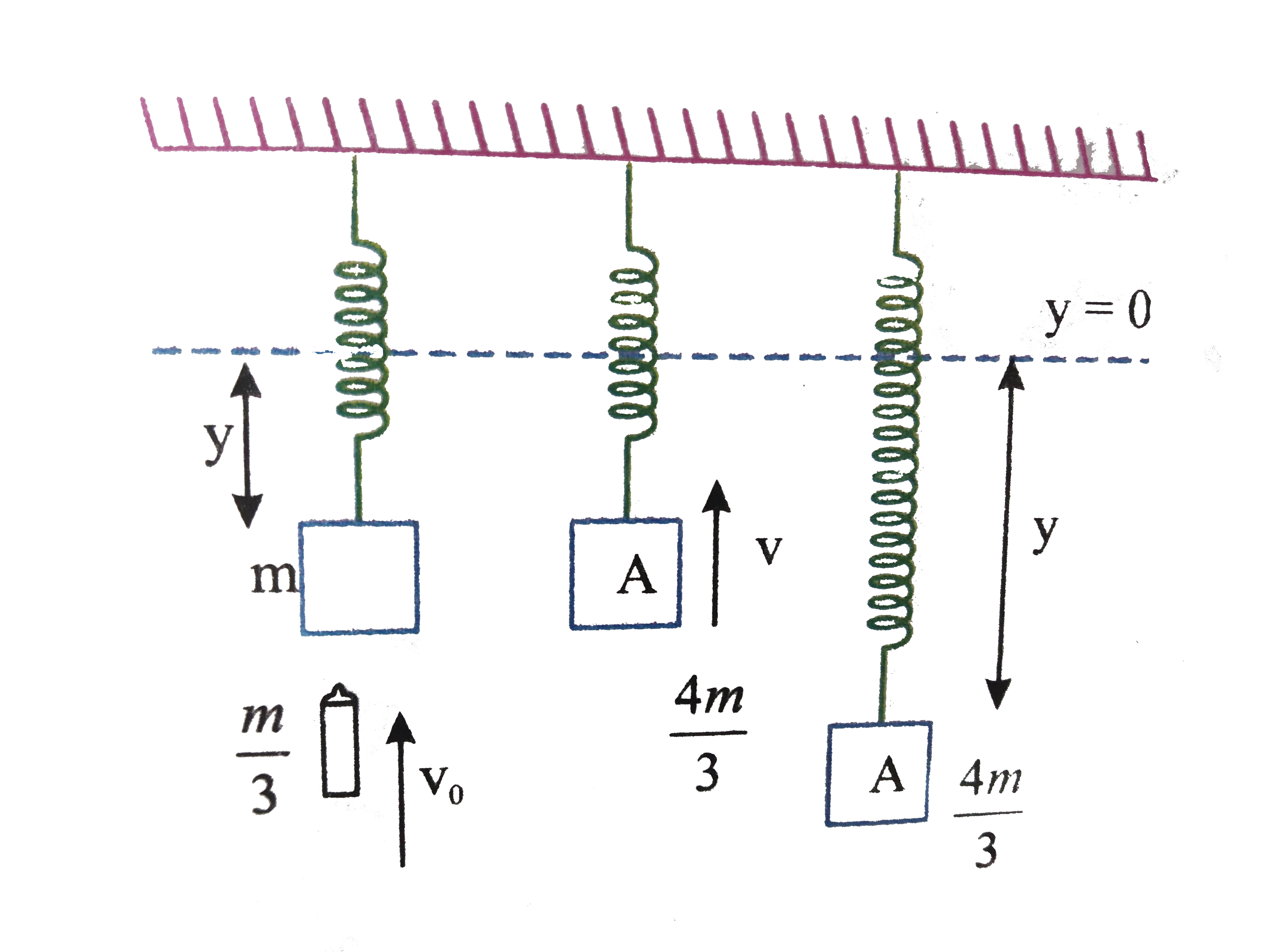
As the bullet strikes the block with velocity `v_(0)` and gets embedded into it, the velocity of the combined mass can be computed bu using the principle of momentum conservation.
`(m)/(3) V_(0) =(4m)/(3)V rArr v = (v_(0))/(4)`
Let new mean position is at distance `y` form origin, then `ky = (4m)/(3)g rArr y = (4mg)/(3k)`.Now, the block executes `S.H.M.` about mean position defined by `y =(4mg)/(3k)`. At `t = 0`, the combined mass is at a displacement of `y -y_(0)` from mean position and is moving with velocity `v`, then by using `v = omega sqrt(A^(2) -x^(2))`, we can fined the amplitude of motion.
`((v_(0))/(4))^(2) = (3k)/(4m) [A^(2) -(y-y_(0))^(2)] = (3k)/(4m) [A^(2) -((mg)/(3k))^(2)]`
`rArr (mv_(0)^(2))/(12k) = A^(2) - ((mg)/(3k))^(2) rArr A = sqrt((mv_(0)^(2))/(12k)+((mg)/(3k))^(2))`
To compute the time taken by the combined mass from `y = (mg)/(k)` to `y = 0`, we can either go for equation method or circular motion projection method:
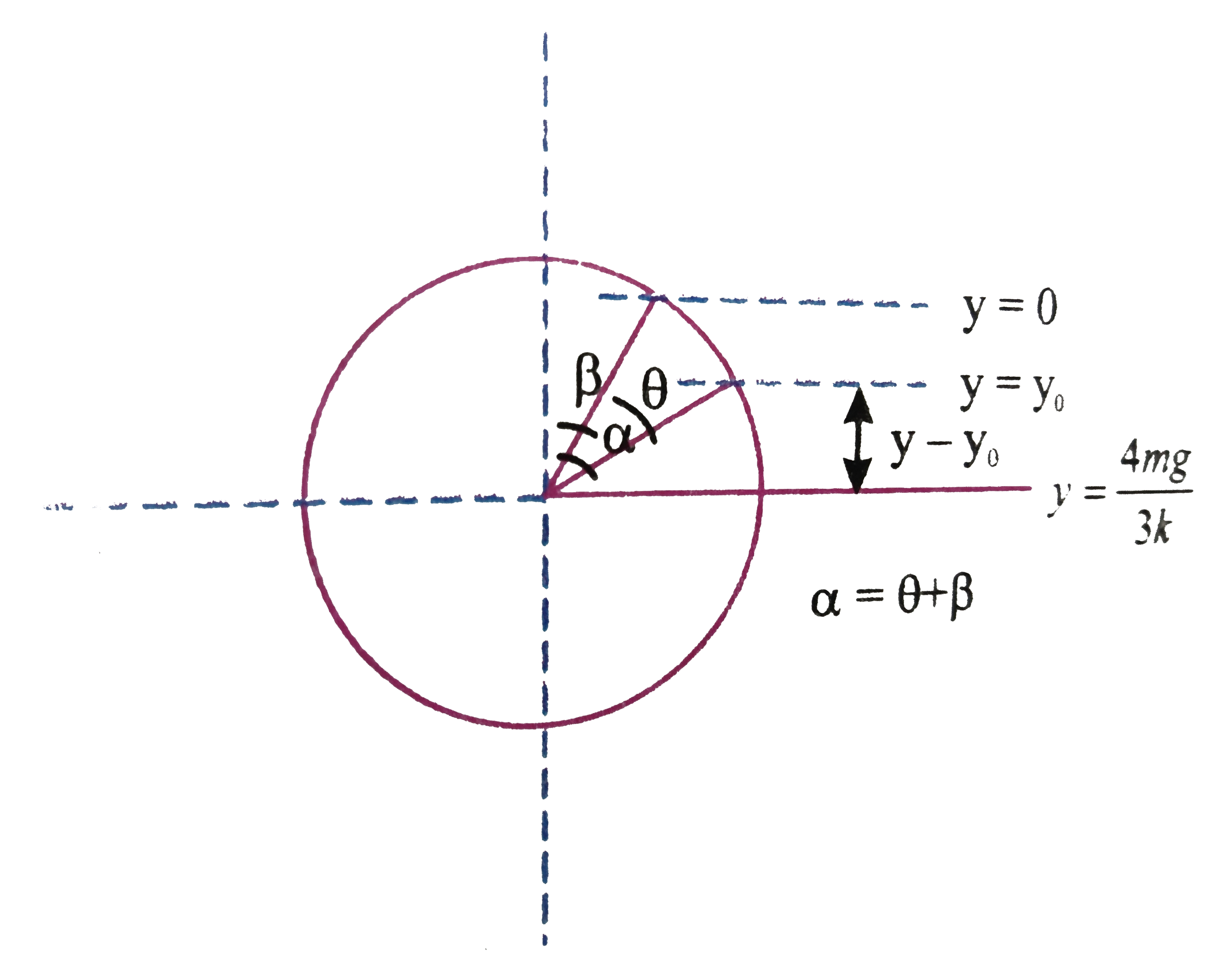
Required time, `t = (theta)/(omega) =(alpha-beta)/(omega)`
`cos alpha =(y -y_(0))/(A) = (mg)/(3kA), cos beta = (y)/(A) = (4mg)/(3kA)`
so, `t = (cos^(-1)((mg)/(3kA))-cos^(-1)((4mg)/(3kA)))/(omega)`
`= sqrt((4m)/(3k)) [cos^(-1) ((mg)/(3kA)) -cos^(-1) ((4mg)/(3kA))]`

As the bullet strikes the block with velocity `v_(0)` and gets embedded into it, the velocity of the combined mass can be computed bu using the principle of momentum conservation.
`(m)/(3) V_(0) =(4m)/(3)V rArr v = (v_(0))/(4)`
Let new mean position is at distance `y` form origin, then `ky = (4m)/(3)g rArr y = (4mg)/(3k)`.Now, the block executes `S.H.M.` about mean position defined by `y =(4mg)/(3k)`. At `t = 0`, the combined mass is at a displacement of `y -y_(0)` from mean position and is moving with velocity `v`, then by using `v = omega sqrt(A^(2) -x^(2))`, we can fined the amplitude of motion.
`((v_(0))/(4))^(2) = (3k)/(4m) [A^(2) -(y-y_(0))^(2)] = (3k)/(4m) [A^(2) -((mg)/(3k))^(2)]`
`rArr (mv_(0)^(2))/(12k) = A^(2) - ((mg)/(3k))^(2) rArr A = sqrt((mv_(0)^(2))/(12k)+((mg)/(3k))^(2))`
To compute the time taken by the combined mass from `y = (mg)/(k)` to `y = 0`, we can either go for equation method or circular motion projection method:

Required time, `t = (theta)/(omega) =(alpha-beta)/(omega)`
`cos alpha =(y -y_(0))/(A) = (mg)/(3kA), cos beta = (y)/(A) = (4mg)/(3kA)`
so, `t = (cos^(-1)((mg)/(3kA))-cos^(-1)((4mg)/(3kA)))/(omega)`
`= sqrt((4m)/(3k)) [cos^(-1) ((mg)/(3kA)) -cos^(-1) ((4mg)/(3kA))]`
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass (m)/(3) moving in vertical up wards direction with velocity v_0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question: Q. The amplitude of oscillation would be
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass (m)/(3) moving in vertical up wards direction with velocity v_0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question: Q. The time taken by the block bullet system to move from y=(mg)/(k) (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
A block of mass m suspended from a spring of spring constant k . Find the amplitude of S.H.M.
A body of mass m is suspended from a massless spring of natural length l . It stretches the spring through a vertical distance y . The potential energy of the stretched spring is
A bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
A bullet of mass m moving with velocity v strikes a suspended wooden block of mass M . If the block rises to a height h , the initial velocity of the block will be (
A bullet of mass m moving horizontally with a velocity v strikes a block of wood of mass M and gets embedded in the block. The block is suspended from the ceiling by a massless string. The height to which block rises is